题目内容
2.解方程组(1)$\left\{\begin{array}{l}{x+y=3}\\{y+z=4}\\{z+x=5}\end{array}\right.$
(2)$\left\{\begin{array}{l}{3x+4x=7}\\{2x+3y+z=9}\\{5x-9y+7z=8}\end{array}\right.$.
分析 (1)①+②+③求出x+y+z=6④,④-①求出z,④-②求出x,④-③求出y;
(2)先求出x,即可得出二元一次方程组,求出方程组的解即可.
解答 解:(1)$\left\{\begin{array}{l}{x+y=3①}\\{y+z=4②}\\{z+x=5③}\end{array}\right.$
①+②+③得:2x+2y+2z=12,
x+y+z=6④,
④-①得:z=3,
④-②得:x=2,
④-③得:y=1,
所以原方程的解为:$\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=3}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{3x+4x=7①}\\{2x+3y+z=9②}\\{5x-9y+7z=8③}\end{array}\right.$
由①得:x=1,
把x=1代入②得:3y+z=7④,
把x=1代入③得:-9y+7z=3⑤,
由④和⑤组成方程组$\left\{\begin{array}{l}{3y+z=7}\\{-9y+7z=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{y=\frac{23}{15}}\\{z=\frac{12}{5}}\end{array}\right.$,
所以原方程组的解为:$\left\{\begin{array}{l}{x=1}\\{y=\frac{23}{15}}\\{z=\frac{12}{5}}\end{array}\right.$.
点评 本题考查了解三元一次方程组,能把三元一次方程组转化成二元一次方程组或一元一次方程是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.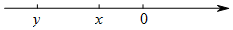 已知x,y两个实数在数轴上位置如图所示,则|y-x|+$\sqrt{{{(x-y)}^2}}$=( )
已知x,y两个实数在数轴上位置如图所示,则|y-x|+$\sqrt{{{(x-y)}^2}}$=( )
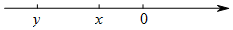 已知x,y两个实数在数轴上位置如图所示,则|y-x|+$\sqrt{{{(x-y)}^2}}$=( )
已知x,y两个实数在数轴上位置如图所示,则|y-x|+$\sqrt{{{(x-y)}^2}}$=( )| A. | 2x | B. | 2y | C. | 2x-2y | D. | 2y-2x |
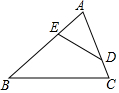 如图,在△ABC中,D,E分别是AC和AB上的点,AD=3cm,AC=4cm,AE=2cm,且$\frac{AD}{AB}$=$\frac{AE}{AC}$,则AB=6cm,BE=4cm.
如图,在△ABC中,D,E分别是AC和AB上的点,AD=3cm,AC=4cm,AE=2cm,且$\frac{AD}{AB}$=$\frac{AE}{AC}$,则AB=6cm,BE=4cm.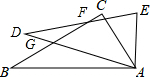 如图,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,BC分别交AD、DE于点G、F,求∠DFB的度数.
如图,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,BC分别交AD、DE于点G、F,求∠DFB的度数.