题目内容
14.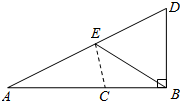 数学课上,老师按下面的方法作线段AB的黄金分割点C(如图),
数学课上,老师按下面的方法作线段AB的黄金分割点C(如图),①过点B作BD⊥AB,使BD=$\frac{1}{2}$AB;
②连结AD,在DA上截取DE=DB;
③在AB上截取AC=AE.
根据上述作图解答下列问题:
(1)如果AB=1,那么AC与BC分别等于多少?
(2)说明点C是线段AB的黄金分割点的理由.
分析 (1)根据题意和勾股定理求出AC与BC的长;
(2)根据黄金分割的比值进行判断即可.
解答 解:(1)∵AB=1,
∴BD=$\frac{1}{2}$,
∴AD=$\sqrt{{1}^{2}+(\frac{1}{2})^{2}}$=$\frac{\sqrt{5}}{2}$,
∴AE=$\frac{\sqrt{5}-1}{2}$,即AC=$\frac{\sqrt{5}-1}{2}$,
BC=AB-AC=$\frac{3-\sqrt{5}}{2}$;
(2)∵$\frac{AC}{AB}$=$\frac{\sqrt{5}-1}{2}$,
∴点C是线段AB的黄金分割点.
点评 本题考查的是黄金分割的概念和勾股定理的应用,掌握把一条线段分成两部分,使其中较长的线段作为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,它们的比值$\frac{\sqrt{5}-1}{2}$叫做黄金比是解题的关键.

练习册系列答案
相关题目
2.10袋小麦称重记录如下,以每袋40kg为准,超出千克数记为正数,不足千克数记为负数,10袋小麦超过多少kg?10袋小麦的重量是多少?
| +7 | +5 | -4 | +6 | +4 | +3 | -3 | -2 | +8 | +1 |
9.若某二次函数的x与y的部分对应值如表:
(1)根据表格,试说明该函数图象的对称轴、顶点坐标和开口方向;
(2)当x为何值时,y随x的增大而增大;
(3)求出该函数的解析式.
| x | -7 | -6 | -5 | -4 | -3 | -2 |
| y | -27 | -13 | -3 | 3 | 5 | 3 |
(2)当x为何值时,y随x的增大而增大;
(3)求出该函数的解析式.
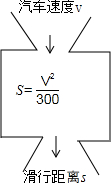 在平整的路面上.某型号汽车紧急刹车后仍将滑行S米,一般地有经验公式S=$\frac{{V}^{2}}{300}$,其中V表示刹车前汽车的速度(单位:千米/时).
在平整的路面上.某型号汽车紧急刹车后仍将滑行S米,一般地有经验公式S=$\frac{{V}^{2}}{300}$,其中V表示刹车前汽车的速度(单位:千米/时).