题目内容
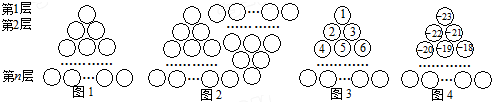
16. 如图所示,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环下去:
如图所示,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环下去:(1)填表:
| 剪的次数 | 1 | 2 | 3 | 4 | 5 |
| 正方形的个数 | 4 | 7 | 10 | 13 | 16 |
(3)如果剪了100次,共剪出多少个小正方形?
分析 (1)观察图形发现规律,利用发现的规律直接写出即可;
(2)根据发现的规律用含有n的代数式表示出即可;
(3)根据(2)中的规律,代入计算即可.
解答 解:(1)填表如下:
| 剪的次数 | 1 | 2 | 3 | 4 | 5 |
| 正方形的个数 | 4 | 7 | 10 | 13 | 16 |
(3)如果剪了100次,共剪出小正方形:3×100+1=301(个).
点评 此题考查图形的变化规律,注意每次都是拿出其中的一个剪成4个正方形,所以相当于在原来的基础上多3个正方形.

练习册系列答案
相关题目
8.下列关系式中,属于二次函数的是(x为自变量)( )
| A. | y=ax2+bx+c | B. | $y=\sqrt{{x^2}-1}$ | C. | $y=\frac{1}{x^2}$ | D. | $y=\frac{1}{8}{x^2}$ |
5.若分式$\frac{{x}^{2}-1}{x-1}$的值为0,则x的取值为( )
| A. | x=1 | B. | x=-1 | C. | x=±1 | D. | 无法确定 |