题目内容
 如图,点B,C,D是⊙O上的定点,点A是动点,且在优弧
如图,点B,C,D是⊙O上的定点,点A是动点,且在优弧 |
| BAD |
| A、0<x<60 |
| B、60<x<120 |
| C、x=120 |
| D、无法确定 |
考点:圆内接四边形的性质,圆周角定理
专题:
分析:先根据圆周角定理用∠BCD表示出∠BAD的度数,再由圆内接四边形的性质求出∠BCD的度数,进而可得出结论.
解答:解:∵∠BAD与∠BOD是同弧所对的圆周角与圆心角,
∴∠BAD=
∠BOD.
∵∠BOD=∠BCD,
∴∠BAD=
∠BCD,
∵四边形ABCD是圆内接四边形,
∴∠BAD+∠BCD=180°,即
∠BCD+∠BCD=180°,解得∠BCD=120°.
∵∠1+∠BAD=180°,
∴∠1=∠BCD=120°.
故选C.
∴∠BAD=
| 1 |
| 2 |
∵∠BOD=∠BCD,
∴∠BAD=
| 1 |
| 2 |
∵四边形ABCD是圆内接四边形,
∴∠BAD+∠BCD=180°,即
| 1 |
| 2 |
∵∠1+∠BAD=180°,
∴∠1=∠BCD=120°.
故选C.
点评:本题考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在△ABC中,AB=5,BC=7,AC=4
如图,在△ABC中,AB=5,BC=7,AC=4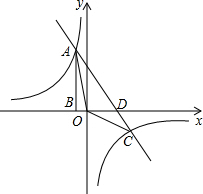 如图,点A是双曲线
如图,点A是双曲线 用三个大写字母表示:∠α可以表示为
用三个大写字母表示:∠α可以表示为