题目内容
11. 如图,已知DE∥BC,O为DE上的点,且DO=BD,EO=EC,连接BO、CO,判断BO、CO是否为∠ABC和∠ACB的平分线.
如图,已知DE∥BC,O为DE上的点,且DO=BD,EO=EC,连接BO、CO,判断BO、CO是否为∠ABC和∠ACB的平分线.
分析 先根据等腰三角形的性质可得∠DBO=∠DOB,∠ECO=∠EOC,再根据平行线的性质得到∠CBO=∠DOB,∠BCO=∠EOC,根据等量代换即可求解.
解答 解:∵DO=BD,EO=EC,
∴∠DBO=∠DOB,∠ECO=∠EOC,
∵DE∥BC,
∴∠CBO=∠DOB,∠BCO=∠EOC,
∴∠CBO=∠OBB,∠BCO=∠OCE,
∴BO、CO是∠ABC和∠ACB的平分线.
点评 本题考查等腰三角形的性质,平行线的性质,以及角平分线的判定,关键是根据题意得到∠CBO=∠OBB,∠BCO=∠OCE,综合性较强,难度一般.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
5.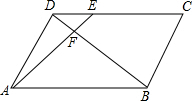 如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD相交于点F,DE:EC=2:3,则S△DEF:S△ABF等于( )
如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD相交于点F,DE:EC=2:3,则S△DEF:S△ABF等于( )
 如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD相交于点F,DE:EC=2:3,则S△DEF:S△ABF等于( )
如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD相交于点F,DE:EC=2:3,则S△DEF:S△ABF等于( )| A. | 4:25 | B. | 4:9 | C. | 9:25 | D. | 2:3 |
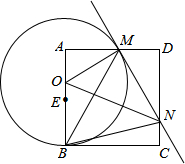 如图,已知正方形ABCD,点E是边AB上一点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连结OM、ON、BM、BN.
如图,已知正方形ABCD,点E是边AB上一点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连结OM、ON、BM、BN. 如图,若直线y=x被双曲线y=$\frac{{k}^{2}}{x}$与双曲线y=$\frac{2{k}^{2}}{x}$在第一象限截得的线段长为2-$\sqrt{2}$.
如图,若直线y=x被双曲线y=$\frac{{k}^{2}}{x}$与双曲线y=$\frac{2{k}^{2}}{x}$在第一象限截得的线段长为2-$\sqrt{2}$.