题目内容
3.有正方形、正六边形、正七边形、正八边形中,用一种就能铺满地面的正多边形是正方形、正六边形.分析 平面图形镶嵌的条件:判断一种图形是否能够镶嵌,只要看一看拼在同一顶点处的几个角能否构成周角.若能构成360°,则说明能够进行平面镶嵌;反之则不能.
解答 解:∵用一种正多边形镶嵌,只有正三角形,正四边形,正六边形三种正多边形能镶嵌成一个平面图案,
∴用同一种正多边形瓷砖铺地面,能铺满地面的正多边形是正方形、正六边形.
故答案为:正方形、正六边形.
点评 此题主要考查了平面镶嵌,用一种正多边形镶嵌,只有正三角形,正四边形,正六边形三种正多边形能镶嵌成一个平面图案.

练习册系列答案
相关题目
17.若一个多边形的内角和是外角和的3倍,则这个正多边形的边数是( )
| A. | 10 | B. | 9 | C. | 8 | D. | 6 |
 如图,已知DE∥BC,O为DE上的点,且DO=BD,EO=EC,连接BO、CO,判断BO、CO是否为∠ABC和∠ACB的平分线.
如图,已知DE∥BC,O为DE上的点,且DO=BD,EO=EC,连接BO、CO,判断BO、CO是否为∠ABC和∠ACB的平分线.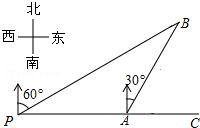 如图,某船从观测站P以每小时4海里的速度航行1小时到达港口A,再沿北偏东30°方向航行一段距离后到达港口B处,此时从观测点P处测得该船位于北偏东60°的方向,求港口B与观测站P之间的距离.
如图,某船从观测站P以每小时4海里的速度航行1小时到达港口A,再沿北偏东30°方向航行一段距离后到达港口B处,此时从观测点P处测得该船位于北偏东60°的方向,求港口B与观测站P之间的距离.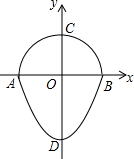 如图,是一个半圆和抛物线的一部分围成的“芒果”,已知点A、B、C、D分别是“芒果”与坐标轴的交点,AB是半圆的直径,抛物线的解析式为y=$\frac{3}{2}$x2-$\frac{3}{2}$,则图中CD的长为$\frac{5}{2}$.
如图,是一个半圆和抛物线的一部分围成的“芒果”,已知点A、B、C、D分别是“芒果”与坐标轴的交点,AB是半圆的直径,抛物线的解析式为y=$\frac{3}{2}$x2-$\frac{3}{2}$,则图中CD的长为$\frac{5}{2}$.