题目内容
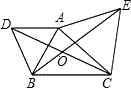 已知:如图,以△ABC的两边AB、AC为边向外作等边△ADB和等边△AEC,DC、BE交于点O.
已知:如图,以△ABC的两边AB、AC为边向外作等边△ADB和等边△AEC,DC、BE交于点O.(1)求证:DC=BE;
(2)求∠BOC的度数;
(3)当∠BAC的度数变化时,∠BOC的度数是否变化.
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)易证∠DAB=∠EAC=60°,AD=AB,AE=AC,即可求得∠DAC=∠BAE,即可证明△DAC≌△BAE;
(2)根据(1)中结论可得∠ADC=∠ABE,即可求得∠ODB+∠OBD=∠ADB+∠ABD,根据三角形外角性质即可解题;
(3)由(2)可得∠ODB+∠OBD=∠ADB+∠ABD,因此可以判定∠BOC和∠BAC大小无关.
(2)根据(1)中结论可得∠ADC=∠ABE,即可求得∠ODB+∠OBD=∠ADB+∠ABD,根据三角形外角性质即可解题;
(3)由(2)可得∠ODB+∠OBD=∠ADB+∠ABD,因此可以判定∠BOC和∠BAC大小无关.
解答:(1)证明:∵△ADB和△AEC都是等边三角形,
∴∠DAB=∠EAC=60°,AD=AB,AE=AC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS);
(2)解:∵△DAC≌△BAE,
∴∠ADC=∠ABE,
∴∠ODB+∠OBD=∠ADB-∠ADC+∠ABD+∠ABE=∠ADB+∠ABD=120°,
∴∠BOC=∠ODB+∠OBD=120°,
(3)解:∵由(2)可得∠ODB+∠OBD=∠ADB+∠ABD,
∴∠BOC和∠BAC大小无关.
∴∠DAB=∠EAC=60°,AD=AB,AE=AC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
|
∴△DAC≌△BAE(SAS);
(2)解:∵△DAC≌△BAE,
∴∠ADC=∠ABE,
∴∠ODB+∠OBD=∠ADB-∠ADC+∠ABD+∠ABE=∠ADB+∠ABD=120°,
∴∠BOC=∠ODB+∠OBD=120°,
(3)解:∵由(2)可得∠ODB+∠OBD=∠ADB+∠ABD,
∴∠BOC和∠BAC大小无关.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△DAC≌△BAE是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
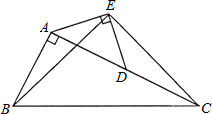 如图,在Rt△ABC中,∠BAC=90°,AB=AD,点D是AC的中点,将一块等腰直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
如图,在Rt△ABC中,∠BAC=90°,AB=AD,点D是AC的中点,将一块等腰直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.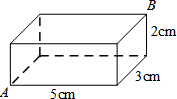 如图,已知长方体的长、宽、高分别是5cm、3cm、2cm,一只蚂蚁要从长方体盒子的一个顶点A处,沿着长方体的表面到长方体和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是
如图,已知长方体的长、宽、高分别是5cm、3cm、2cm,一只蚂蚁要从长方体盒子的一个顶点A处,沿着长方体的表面到长方体和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是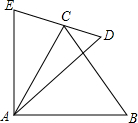 已知,如图AE=AC,AD=AB,∠EAC=∠DAB.求证:
已知,如图AE=AC,AD=AB,∠EAC=∠DAB.求证:
 如图所示,△ABC是等边三角形,延长AC到D,以BD为边作等边△BDE,连接AE.
如图所示,△ABC是等边三角形,延长AC到D,以BD为边作等边△BDE,连接AE.