题目内容
 如图所示,△ABC是等边三角形,延长AC到D,以BD为边作等边△BDE,连接AE.
如图所示,△ABC是等边三角形,延长AC到D,以BD为边作等边△BDE,连接AE.证明:(1)△ABE≌△CBD;
(2)AD=AE+AB.
考点:全等三角形的判定与性质,等边三角形的性质
专题:证明题
分析:(1)易证AB=BC,BE=BD,∠ABC=∠EBD=60°,可得∠ABE=∠CBD,即可证明△ABE≌△CBD;
(2)根据(1)中结论可得AE=CD,易证AB=AC,即可解题.
(2)根据(1)中结论可得AE=CD,易证AB=AC,即可解题.
解答:证明:(1)∵△ABC,△BDE是等边三角形,
∴AB=BC,BE=BD,∠ABC=∠EBD=60°,
∵∠ABE+∠CBE=60°,∠CBE+∠CBD=60°,
∴∠ABE=∠CBD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS);
(2)∵△ABE≌△CBD,
∴AE=CD,
∵△ABC是等边三角形,
∴AB=AC,
∵AD=AC+CD,
∴AD=AB+AE.
∴AB=BC,BE=BD,∠ABC=∠EBD=60°,
∵∠ABE+∠CBE=60°,∠CBE+∠CBD=60°,
∴∠ABE=∠CBD,
在△ABE和△CBD中,
|
∴△ABE≌△CBD(SAS);
(2)∵△ABE≌△CBD,
∴AE=CD,
∵△ABC是等边三角形,
∴AB=AC,
∵AD=AC+CD,
∴AD=AB+AE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABE≌△CBD是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
已知一元二次方程x2-8x+15=0的两个根分别是Rt△ABC的两边长,则第3条边长( )
| A、3 | ||
| B、4或5 | ||
| C、3或5 | ||
D、4或
|
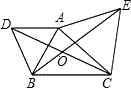 已知:如图,以△ABC的两边AB、AC为边向外作等边△ADB和等边△AEC,DC、BE交于点O.
已知:如图,以△ABC的两边AB、AC为边向外作等边△ADB和等边△AEC,DC、BE交于点O. 如图,已知⊙O的直径AB=d,弦AC=a,
如图,已知⊙O的直径AB=d,弦AC=a,