题目内容
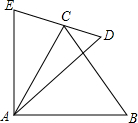 已知,如图AE=AC,AD=AB,∠EAC=∠DAB.求证:
已知,如图AE=AC,AD=AB,∠EAC=∠DAB.求证:(1)△EAD≌△CAB;
(2)∠DCB=∠BAD.
考点:全等三角形的判定与性质,三角形内角和定理
专题:证明题
分析:(1)易证∠EAD=∠CAB,即可证明△EAD≌△CAB;
(2)根据(1)中结论可得∠E=∠ACB,根据∠ACD=∠E+∠EAC,即可求得∠DCB=∠EAC,即可解题.
(2)根据(1)中结论可得∠E=∠ACB,根据∠ACD=∠E+∠EAC,即可求得∠DCB=∠EAC,即可解题.
解答:证明:(1)∵∠EAC=∠DAB,
∴∠EAC+∠CAD=∠DAB+∠CAD,即∠EAD=∠CAB,
在△EAD和△CAB中,
,
∴△EAD≌△CAB(SAS);
(2)∵△EAD≌△CAB,
∴∠E=∠ACB,
∵∠ACD=∠E+∠EAC,
∴∠ACB+∠DCB=∠E+∠EAC,
∴∠DCB=∠EAC,
∵∠EAC=∠DAB,
∴∠DCB=∠BAD.
∴∠EAC+∠CAD=∠DAB+∠CAD,即∠EAD=∠CAB,
在△EAD和△CAB中,
|
∴△EAD≌△CAB(SAS);
(2)∵△EAD≌△CAB,
∴∠E=∠ACB,
∵∠ACD=∠E+∠EAC,
∴∠ACB+∠DCB=∠E+∠EAC,
∴∠DCB=∠EAC,
∵∠EAC=∠DAB,
∴∠DCB=∠BAD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△EAD≌△CAB是解题的关键.

练习册系列答案
相关题目
已知一元二次方程x2-8x+15=0的两个根分别是Rt△ABC的两边长,则第3条边长( )
| A、3 | ||
| B、4或5 | ||
| C、3或5 | ||
D、4或
|
 已知:如图,以△ABC的两边AB、AC为边向外作等边△ADB和等边△AEC,DC、BE交于点O.
已知:如图,以△ABC的两边AB、AC为边向外作等边△ADB和等边△AEC,DC、BE交于点O. 如图,在△ABC中,∠ACB=90°,∠A=20°,若将△ABC沿CD折叠,使点B落在AC边上的E处,则∠ADE的度数是
如图,在△ABC中,∠ACB=90°,∠A=20°,若将△ABC沿CD折叠,使点B落在AC边上的E处,则∠ADE的度数是 如图,将一副三角板叠放在一起,使直角顶点重合于O(即∠COD=∠BOA=90°).请问∠BOD与∠AOC有什么关系?并说明理由.
如图,将一副三角板叠放在一起,使直角顶点重合于O(即∠COD=∠BOA=90°).请问∠BOD与∠AOC有什么关系?并说明理由. 如图,已知⊙O的直径AB=d,弦AC=a,
如图,已知⊙O的直径AB=d,弦AC=a,