题目内容
如图,在直角坐标系xOy中,直线AB交x轴于A(2,0),交y轴负半轴于B(0,-10),C为x轴正半轴上一点,且OC=5OA.
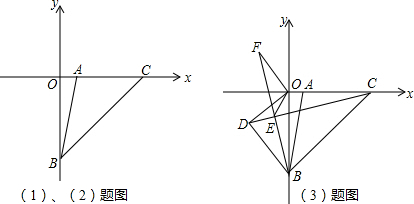
(1)求△ABC的面积;
(2)延长BA到P(自己补全图形),使得PA=AB,过点P作PM⊥OC于M,求P点的坐标;
(3)如图,D是第三象限内一动点,直线BE⊥CD于E,OF⊥OD交BE延长线于F.当D点运动时,
的大小是否发生变化?若改变,请说明理由;若不变,求出这个比值.

(1)求△ABC的面积;
(2)延长BA到P(自己补全图形),使得PA=AB,过点P作PM⊥OC于M,求P点的坐标;
(3)如图,D是第三象限内一动点,直线BE⊥CD于E,OF⊥OD交BE延长线于F.当D点运动时,
| OD |
| OF |
考点:全等三角形的判定与性质,坐标与图形性质,三角形的面积
专题:
分析:(1)易求OC的长,即可求得AC的长,即可解题;
(2)作出图形,易证△PAM≌△BAO,可得PM=OB,AM=OA,即可解题;
(3)易证∠OCD=∠OBF和∠COD=∠BOF,即可证明△CDO≌△BFO,可得DO=FO,即可解题.
(2)作出图形,易证△PAM≌△BAO,可得PM=OB,AM=OA,即可解题;
(3)易证∠OCD=∠OBF和∠COD=∠BOF,即可证明△CDO≌△BFO,可得DO=FO,即可解题.
解答:解:(1)∵OC=5AO,AO=2,
∴OC=10,
∴AC=OC-OA=8,
∴S△ABC=
AC•OB=
×8×10=40;
(2)作出图形,
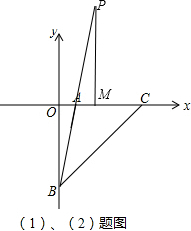
在△PAM和△BAO中,
,
∴△PAM≌△BAO(AAS),
∴PM=OB=10,AM=OA=2,
∴点P坐标为(4,10);
(3)如图,
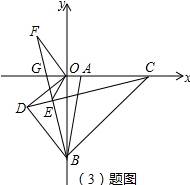
∵∠OCD+∠OGE=90°,∠OFE+∠OBF=90°,
∴∠OCD=∠OBF,
∵∠FOG+∠DOG=90°,∠DOG+∠BOD=90°,
∴∠BOD=∠FOG,
∵∠BOC=∠BOG=90°,
∴∠BOD+90°=∠FOG+90°,即∠COD=∠BOF,
在△CDO和△BFO中,
,
∴△CDO≌△BFO(ASA),
∴DO=FO,
∴
=1.
∴OC=10,
∴AC=OC-OA=8,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
(2)作出图形,

在△PAM和△BAO中,
|
∴△PAM≌△BAO(AAS),
∴PM=OB=10,AM=OA=2,
∴点P坐标为(4,10);
(3)如图,

∵∠OCD+∠OGE=90°,∠OFE+∠OBF=90°,
∴∠OCD=∠OBF,
∵∠FOG+∠DOG=90°,∠DOG+∠BOD=90°,
∴∠BOD=∠FOG,
∵∠BOC=∠BOG=90°,
∴∠BOD+90°=∠FOG+90°,即∠COD=∠BOF,
在△CDO和△BFO中,
|
∴△CDO≌△BFO(ASA),
∴DO=FO,
∴
| OD |
| OF |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△PAM≌△BAO和△CDO≌△BFO是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 如图,在⊙O中,AD∥BC,AC⊥BD垂足为E.
如图,在⊙O中,AD∥BC,AC⊥BD垂足为E.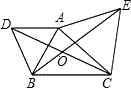 已知:如图,以△ABC的两边AB、AC为边向外作等边△ADB和等边△AEC,DC、BE交于点O.
已知:如图,以△ABC的两边AB、AC为边向外作等边△ADB和等边△AEC,DC、BE交于点O. 如图,在△ABC中,∠ACB=90°,∠A=20°,若将△ABC沿CD折叠,使点B落在AC边上的E处,则∠ADE的度数是
如图,在△ABC中,∠ACB=90°,∠A=20°,若将△ABC沿CD折叠,使点B落在AC边上的E处,则∠ADE的度数是 如图,将一副三角板叠放在一起,使直角顶点重合于O(即∠COD=∠BOA=90°).请问∠BOD与∠AOC有什么关系?并说明理由.
如图,将一副三角板叠放在一起,使直角顶点重合于O(即∠COD=∠BOA=90°).请问∠BOD与∠AOC有什么关系?并说明理由.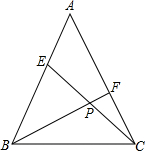 等腰△ABC中,AB=AC,E、F分别是AB、AC上的点,且BE=AF,连接CE、BF交于点P.若
等腰△ABC中,AB=AC,E、F分别是AB、AC上的点,且BE=AF,连接CE、BF交于点P.若 如图,已知⊙O的直径AB=d,弦AC=a,
如图,已知⊙O的直径AB=d,弦AC=a,