题目内容
6.化简下列各式(1)$\sqrt{18}$-$\sqrt{12}$-$\sqrt{2}$+$\frac{1}{\sqrt{3}}$;
(2)$\sqrt{24}$+4$\sqrt{\frac{3}{8}}$-$\sqrt{3}$×$\sqrt{18}$+$\frac{\sqrt{6}}{3}$×$\sqrt{75}$÷$\frac{1}{\sqrt{2}}$.
分析 (1)根据二次根式的加减法可以解答本题;
(2)根据二次根式的乘除法和加减法可以解答本题.
解答 解:(1)$\sqrt{18}$-$\sqrt{12}$-$\sqrt{2}$+$\frac{1}{\sqrt{3}}$
=$3\sqrt{2}-2\sqrt{3}-\sqrt{2}+\frac{\sqrt{3}}{3}$
=$2\sqrt{2}-\frac{5\sqrt{3}}{3}$;
(2)$\sqrt{24}$+4$\sqrt{\frac{3}{8}}$-$\sqrt{3}$×$\sqrt{18}$+$\frac{\sqrt{6}}{3}$×$\sqrt{75}$÷$\frac{1}{\sqrt{2}}$
=$2\sqrt{6}+\sqrt{6}-3\sqrt{6}+5\sqrt{2}×\sqrt{2}$
=$2\sqrt{6}+\sqrt{6}-3\sqrt{6}+10$
=10.
点评 本题考查二次根式的混合运算,解答本题的关键是明确二次根式的混合运算的解答方法.

练习册系列答案
相关题目
16.下列命题中,假命题是( )
| A. | 对角线相等的菱形是正方形 | |
| B. | 对角线互相垂直的矩形是正方形 | |
| C. | 对角线互相垂直且相等的平行四边形是正方形 | |
| D. | 对角线互相垂直且相等的四边形是正方形 |
17.有甲、乙两个箱子,甲箱内有90颗球,分别标记号码1~90,号码为不重复的整数,乙箱内没有球.已知小李从甲箱内拿出45颗球放入乙箱后,乙箱内球的号码的中位数为30.若此时甲箱内有a颗球的号码小于30,有b颗球的号码大于30,则关于a、b正确的是( )
| A. | a=8 | B. | a=22 | C. | b=22 | D. | b=38 |
14.下列命题中,原命题与逆命题均为真命题的有( )
①若|a|=|b|,则a2=b2;②若ma2>na2,则m>n;
③对顶角相等;④对角线互相平分的四边形是平行四边形.
①若|a|=|b|,则a2=b2;②若ma2>na2,则m>n;
③对顶角相等;④对角线互相平分的四边形是平行四边形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.等腰三角形两边的长分别为3cm和5cm,则这个三角形的周长是( )
| A. | 11cm | B. | 13cm | C. | 11cm或13cm | D. | 不确定 |
11. 五子棋的比赛规则是一人执黑子,一人执白子,两人轮流出棋,每次放一个棋子在棋盘的格点处,只要有同色的五个棋子先连成一条线(横、竖、斜均可)就获得胜利.如图是两人正在玩的一盘棋,若白棋A所在点的坐标是(-2,2),黑棋B所在点的坐标是(0,4),现在轮到黑棋走,黑棋放到点C的位置就获得胜利,点C的坐标是( )
五子棋的比赛规则是一人执黑子,一人执白子,两人轮流出棋,每次放一个棋子在棋盘的格点处,只要有同色的五个棋子先连成一条线(横、竖、斜均可)就获得胜利.如图是两人正在玩的一盘棋,若白棋A所在点的坐标是(-2,2),黑棋B所在点的坐标是(0,4),现在轮到黑棋走,黑棋放到点C的位置就获得胜利,点C的坐标是( )
 五子棋的比赛规则是一人执黑子,一人执白子,两人轮流出棋,每次放一个棋子在棋盘的格点处,只要有同色的五个棋子先连成一条线(横、竖、斜均可)就获得胜利.如图是两人正在玩的一盘棋,若白棋A所在点的坐标是(-2,2),黑棋B所在点的坐标是(0,4),现在轮到黑棋走,黑棋放到点C的位置就获得胜利,点C的坐标是( )
五子棋的比赛规则是一人执黑子,一人执白子,两人轮流出棋,每次放一个棋子在棋盘的格点处,只要有同色的五个棋子先连成一条线(横、竖、斜均可)就获得胜利.如图是两人正在玩的一盘棋,若白棋A所在点的坐标是(-2,2),黑棋B所在点的坐标是(0,4),现在轮到黑棋走,黑棋放到点C的位置就获得胜利,点C的坐标是( )| A. | (3,3) | B. | (3,2) | C. | (5,2) | D. | (4,3) |
18. 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),点D的坐标为(2,0),E为AB上的点,当△CDE的周长最小时,点E的坐标为( )
矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),点D的坐标为(2,0),E为AB上的点,当△CDE的周长最小时,点E的坐标为( )
 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),点D的坐标为(2,0),E为AB上的点,当△CDE的周长最小时,点E的坐标为( )
矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),点D的坐标为(2,0),E为AB上的点,当△CDE的周长最小时,点E的坐标为( )| A. | (1,3) | B. | (3,1) | C. | (4,1) | D. | (3,2) |
16.对某批乒乓球的质量进行随机调查,结果如下表:
根据上表,在这批乒乓球中任取一个,它为优等品的概率大约是0.82.
| 随机抽取的乒乓球数n | 10 | 20 | 50 | 100 | 200 | 500 | 1000 |
| 优等品数m | 7 | 16 | 43 | 81 | 164 | 410 | 820 |
| 优等品率$\frac{m}{n}$ | 0.7 | 0.8 | 0.86 | 0.81 | 0.82 | 0.82 | 0.82 |
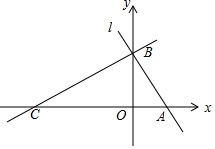 如图,平面直角坐标系中,直线l:y=-$\sqrt{3}$x+$\sqrt{3}$分别交x轴,y轴于A,B两点,点C在x轴负半轴上,且∠ACB=30°.
如图,平面直角坐标系中,直线l:y=-$\sqrt{3}$x+$\sqrt{3}$分别交x轴,y轴于A,B两点,点C在x轴负半轴上,且∠ACB=30°.