题目内容
15.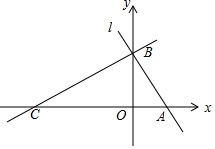 如图,平面直角坐标系中,直线l:y=-$\sqrt{3}$x+$\sqrt{3}$分别交x轴,y轴于A,B两点,点C在x轴负半轴上,且∠ACB=30°.
如图,平面直角坐标系中,直线l:y=-$\sqrt{3}$x+$\sqrt{3}$分别交x轴,y轴于A,B两点,点C在x轴负半轴上,且∠ACB=30°.(1)求A,C两点的坐标.
(2)若点M从点C出发,以每秒1个单位长度的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,求出S关于t的函数关系式,并写出自变量的取值范围.
(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A,B,P,Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,说明理由.
分析 (1)由直线方程易得点A的坐标.在直角△BOC中,利用30度所对的直角边等于斜边的一半求出BC的长,利用勾股定理求出OC的长,确定出C的坐标即可;
(2)先求出∠ABC=90°,分两种情况考虑:当M在线段BC上;当M在线段BC延长线上;表示出BM,利用三角形面积公式分别表示出S与t的函数关系式即可;
(3)点P是y轴上的点,在坐标平面内存在点Q,使以A、B、P、Q为顶点的四边形是菱形,分两种情况,如图所示,利用菱形的性质求出AQ的长,根据AQ与y轴平行得到Q与A横坐标相同,求出满足题意Q得坐标即可.
解答  解:(1)当x=0时,y=$\sqrt{3}$;当y=0时,x=1.
解:(1)当x=0时,y=$\sqrt{3}$;当y=0时,x=1.
∴点A坐标为(1,0),点B坐标为(0,$\sqrt{3}$),
在Rt△BOC中,∠OCB=30°,OB=$\sqrt{3}$,
∴BC=2$\sqrt{3}$.
∴OC=$\sqrt{(2\sqrt{3})^{2}-(\sqrt{3})^{2}}$=3.
∴点C坐标为(-3,0).
(2)如图1所示:∵OA=1,OB=$\sqrt{3}$,AB=2,
∴∠ABO=30°,
同理:BC=2$\sqrt{3}$,∠OCB=30°,
∴∠OBC=60°,
∴∠ABC=90°,
分两种情况考虑:若M在线段BC上时,BC=2$\sqrt{3}$,CM=t,可得BM=BC-CM=2$\sqrt{3}$-t,
此时S△ABM=$\frac{1}{2}$BM•AB=$\frac{1}{2}$×(2$\sqrt{3}$-t)×2=2$\sqrt{3}$-t(0≤t<2$\sqrt{3}$);
若M在BC延长线上时,BC=2$\sqrt{3}$,CM=t,可得BM=CM-BC=t-2$\sqrt{3}$,
此时S△ABM=$\frac{1}{2}$BM•AB=$\frac{1}{2}$×(t-2$\sqrt{3}$)×2=t-2$\sqrt{3}$(t≥2$\sqrt{3}$);
综上所述,S=$\left\{\begin{array}{l}{2\sqrt{3}-t(0≤t<2\sqrt{3})}\\{t-2\sqrt{3}(t≥2\sqrt{3})}\end{array}\right.$;
(3)P是y轴上的点,在坐标平面内存在点Q,使以 A、B、P、Q为顶点的四边形是菱形,
如2图所示,
当P在y轴正半轴上,四边形ABPQ为菱形,①可得AQ=AB=2,且Q与A的横坐标相同,
此时Q坐标为(1,2),②AP=AQ=$\frac{2\sqrt{3}}{3}$,Q与A的横坐标相同,此时Q坐标为(1,$\frac{2\sqrt{3}}{3}$),
当P在y轴负半轴上,四边形ABPQ为菱形,①可得AQ=AB=2,且Q与A横坐标相同,
此时Q坐标为(1,-2),②BP垂直平分AQ,此时Q坐标为(-1,0),
综上,满足题意Q坐标为(1,2)、(1,-2)、(1,$\frac{2\sqrt{3}}{3}$)、(-1,0).
点评 此题属于一次函数综合题,涉及的知识有:含30度直角三角形的性质,勾股定理,坐标与图形性质,待定系数法求一次函数解析式,菱形的性质,利用了分类讨论的思想,熟练掌握待定系数法是解本题第二问的关键.

 如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是( )
如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是( )| A. | ∠ABC=90° | B. | AC=BD | C. | OA=OB | D. | OA=AB |
| A. | 1:2 | B. | 2:5 | C. | 3:5 | D. | 3:4 |
| A. |  | B. |  | C. |  | D. |  |
 如图,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长为x,宽为y,则依题意列二元一次方程组正确的是( )
如图,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长为x,宽为y,则依题意列二元一次方程组正确的是( )| A. | $\left\{\begin{array}{l}{5x+2y=75}\\{y=3x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+y=75}\\{y=3x}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+2y=75}\\{x=3y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=75}\\{x=3y}\end{array}\right.$ |
| A. | 30,40,50 | B. | 7,12,13 | C. | 5,8,10 | D. | 3,4,6 |