题目内容
6. 如图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
分析 通过解直角△BCD和直角△ACD分别求得BD、CD以及AD的长度,则易得AB的长度,则根据题意得到整个过程中旗子上升高度,由“速度=$\frac{上升的高度}{时间}$”进行解答即可.
解答 解:在Rt△BCD中,BD=9米,∠BCD=45°,则BD=CD=9米.
在Rt△ACD中,CD=9米,∠ACD=37°,则AD=CD•tan37°≈9×0.75=6.75(米).
所以,AB=AD+BD=15.75米,
整个过程中旗子上升高度是:15.75-2.25=13.5(米),
因为耗时45s,
所以上升速度v=$\frac{13.5}{45}$=0.3(米/秒).
答:国旗应以0.3米/秒的速度匀速上升.
点评 本题考查了解直角三角形的应用-仰角俯角问题.解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列运算结果正确的是( )
| A. | a2+a3=a5 | B. | a2•a3=a6 | C. | a3÷a2=a | D. | (a2)3=a5 |
17.从-$\sqrt{5}$,0,$\sqrt{4}$,π,3.5这五个数中,随机抽取一个,则抽到无理数的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
1.如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(cm) | 185 | 180 | 185 | 180 |
| 方差 | 3.6 | 3.6 | 7.4 | 8.1 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
19.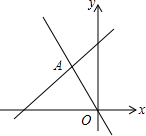 如图,在平面直角坐标系中,直线y=-2x和y=ax+4相交于点A(m,3),则不等式-2x<ax+4的解集为( )
如图,在平面直角坐标系中,直线y=-2x和y=ax+4相交于点A(m,3),则不等式-2x<ax+4的解集为( )
 如图,在平面直角坐标系中,直线y=-2x和y=ax+4相交于点A(m,3),则不等式-2x<ax+4的解集为( )
如图,在平面直角坐标系中,直线y=-2x和y=ax+4相交于点A(m,3),则不等式-2x<ax+4的解集为( )| A. | x<-$\frac{3}{2}$ | B. | x<3 | C. | x>-$\frac{3}{2}$ | D. | x>3 |
 如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x-3分别与x轴、y轴交于点A、B,点P的坐标为(0,4).若点M在直线AB上,则PM长的最小值为$\frac{28}{5}$.
如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x-3分别与x轴、y轴交于点A、B,点P的坐标为(0,4).若点M在直线AB上,则PM长的最小值为$\frac{28}{5}$.