题目内容
18．已知数轴上A，B两点到原点的距离分别是$\sqrt{5}$和1，则AB=$\sqrt{5}$+1或$\sqrt{5}$-1．分析 由于到原点的距离实际表示这个数的绝对值，由此得到数轴上两点间距离的公式便可解答．
解答 解：∵到原点的距离实际表示这个数的绝对值，
而 A、B到原点的距离是$\sqrt{5}$和1，
∴点A表示的数为$\sqrt{5}$或-$\sqrt{5}$，点B表示的数为1或-1，
∴AB=$\sqrt{5}$-1，或AB=$\sqrt{5}$-（-1）=$\sqrt{5}$+1，或AB=1-（-$\sqrt{5}$）=1+$\sqrt{5}$或AB=-1-（-$\sqrt{5}$）=$\sqrt{5}$-1．
故答案为：$\sqrt{5}$+1或$\sqrt{5}$-1．
点评 此题主要考查了是与数轴之间的对应关系，其中绝对值是正数的数有2个．解题关键是求数轴上两点间的距离应让较大的数减去较小的数即可．
练习册系列答案
相关题目
8．下列一组数：1，4，0，$-\frac{1}{2}$，-3在数轴上表示的点中，不在原点右边的点的个数为（ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
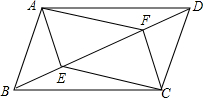如图，?ABCD中，E、F两点都在对角线BD上，且BE=DF．求证：∠EAF=∠ECF．