题目内容
18.给出a的三个值,使一次函数y=ax+2a-1的图象分别经过第一、二、三象限;第二、三、四象限;第一、三、四象限.分析 根据一次函数与系数的关系可得a的取值范围,从而确定a的值.
解答 解:当一次函数y=ax+2a-1的图象分别经过第一、二、三象限时,
a>0且2a-1>0,
解得a$>\frac{1}{2}$,
∴当a=1时,一次函数y=ax+2a-1的图象分别经过第一、二、三象限;
当一次函数y=ax+2a-1的图象分别经过第二、三、四象限时,
a<0且2a-1<0,
解得a<0,
∴当a=-1时,一次函数y=ax+2a-1的图象分别经过第二、三、四象限;
当一次函数y=ax+2a-1的图象分别经过第一、三、四象限时,
a>0且2a-1<0,
解得0<a$<\frac{1}{2}$,
∴当a=$\frac{1}{3}$时,一次函数y=ax+2a-1的图象分别经过第一、三、四象限;
(以上答案不唯一).
点评 本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题的关键是注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限,y随x的增大而增大;k<0时,直线必经过二、四象限,y随x的增大而减小;b>0时,直线与y轴正半轴相交;b=0时,直线过原点;b<0时,直线与y轴负半轴相交.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
1.C919大飞机是中国完全具有自主知识产权的干线民用飞机,其零部件总数超过100万个,请将100万用科学记数法表示为( )
| A. | 1×106 | B. | 100×104 | C. | 1×107 | D. | 0.1×108 |
9.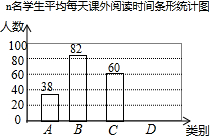 某校开展“百日读书好习惯”活动,校团委为了解学生每天课外阅读情况,随机抽取了n名学生,统计他们平均每天课外阅读时间(单位:时)根据时间的长短分为A,B,C,D四类,并将所得数据绘制成如下统计表及不完整的统计图.
某校开展“百日读书好习惯”活动,校团委为了解学生每天课外阅读情况,随机抽取了n名学生,统计他们平均每天课外阅读时间(单位:时)根据时间的长短分为A,B,C,D四类,并将所得数据绘制成如下统计表及不完整的统计图.
n名学生平均每天课外阅读时间统计表
根据上面统计信息,解答下列问题:
(1)求n的值,并补全条形统计图.
(2)求选择类别B的学生人数占被调查的学生人数的百分比.
(3)根据上述调查结果,估计该校2200名学生平均每天课外阅读时间在1小时以上的人数.
 某校开展“百日读书好习惯”活动,校团委为了解学生每天课外阅读情况,随机抽取了n名学生,统计他们平均每天课外阅读时间(单位:时)根据时间的长短分为A,B,C,D四类,并将所得数据绘制成如下统计表及不完整的统计图.
某校开展“百日读书好习惯”活动,校团委为了解学生每天课外阅读情况,随机抽取了n名学生,统计他们平均每天课外阅读时间(单位:时)根据时间的长短分为A,B,C,D四类,并将所得数据绘制成如下统计表及不完整的统计图.n名学生平均每天课外阅读时间统计表
| 类别 | 时间t(小时) | 人数 |
| A | 0<t≤0.5 | 38 |
| B | 0.5<t≤1 | 82 |
| C | 1<t≤1.5 | 60 |
| D | t>1.5 | 20 |
(1)求n的值,并补全条形统计图.
(2)求选择类别B的学生人数占被调查的学生人数的百分比.
(3)根据上述调查结果,估计该校2200名学生平均每天课外阅读时间在1小时以上的人数.
7. 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
步骤1:分别以点A,D为圆心,以大于$\frac{1}{2}$AD的长为半径,在AD两侧作弧,两弧交于点M,N;
步骤2:连接MN,分别交AB,AC于点E,F;
步骤3:连接DE,DF.
下列叙述不一定成立的是( )
 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:步骤1:分别以点A,D为圆心,以大于$\frac{1}{2}$AD的长为半径,在AD两侧作弧,两弧交于点M,N;
步骤2:连接MN,分别交AB,AC于点E,F;
步骤3:连接DE,DF.
下列叙述不一定成立的是( )
| A. | 线段DE是△ABC的中位线 | B. | 四边形AFDE是菱形 | ||
| C. | MN垂直平分线段AD | D. | $\frac{BD}{DC}$=$\frac{BE}{EA}$ |
 如图,直线y=-2x-4与坐标轴交于A、B两点,点P为直线y=2x上一点,且△ABP的面积被y轴分成1:2的两部分,求点P的坐标.
如图,直线y=-2x-4与坐标轴交于A、B两点,点P为直线y=2x上一点,且△ABP的面积被y轴分成1:2的两部分,求点P的坐标. 已知一次函数y=kx+b的图象经过点A(1,3)和B(-1,-1)两点.
已知一次函数y=kx+b的图象经过点A(1,3)和B(-1,-1)两点. 直线y=kx+b(k≠0)的图象如图所示,由图象可知当y<0时,x的取值范围是x<2.
直线y=kx+b(k≠0)的图象如图所示,由图象可知当y<0时,x的取值范围是x<2.