题目内容
4.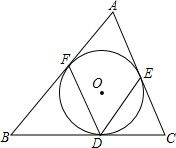 如图,△ABC内,内切圆⊙O与BC,AC,AB分别相切于点D,E,F,若∠FDE=65°,求∠A的度数.
如图,△ABC内,内切圆⊙O与BC,AC,AB分别相切于点D,E,F,若∠FDE=65°,求∠A的度数.
分析 连接OE、OF.由圆周角定理可求得∠EOF的度数,在四边形AEOF中,∠OEA=∠OFA=90°,因此∠A和∠EOF互补,由此可求出∠A的度数.
解答 解:连接OD,OF.
∵AB、AC分别是圆O的切线,
∴∠AEO=∠AFO=90°.
∴∠A+∠EOF=180°.
由圆周角定理知:∠EOF=2∠EDF=130°.
∴∠A=180°-∠EOF=180°-130°=50°.
点评 本题主要考查的是三角的内切圆、圆周角定理,证得∠A+∠EOF=180°是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.在Rt△ABC中,已知∠B=90°,AC=10,AB=5$\sqrt{2}$,则∠A等于( )
| A. | 45° | B. | 30° | C. | 60° | D. | 50° |
13.在直角坐标系中,与点A(2012,-1)关于x轴对称的点的坐标是( )
| A. | (2012,1) | B. | (-2012,-1) | C. | (-2012,1) | D. | (-1,2012) |
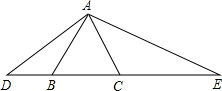 如图,△ABC是等边三角形,∠DAE=120°.求证:
如图,△ABC是等边三角形,∠DAE=120°.求证: