题目内容
11.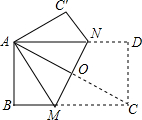 如图,在矩形ABCD中,AD>AB,点M,N分别在BC,AD边上,将矩形ABCD以直线MN为折痕进行折叠,翻折后能使点C恰好与A点重合,△AMN是一个怎样的三角形?请说明理由.
如图,在矩形ABCD中,AD>AB,点M,N分别在BC,AD边上,将矩形ABCD以直线MN为折痕进行折叠,翻折后能使点C恰好与A点重合,△AMN是一个怎样的三角形?请说明理由.
分析 由翻折的性质可知:AO=OC,AM=MC.然后证明依据AAS证明△ANO≌△CMO,故此AN=MC,于是得到AM=AN.
解答 解:△AMN是等腰三角形.
理由:由翻折的性质可知:AO=OC,AM=MC.
∵AD∥BC,
∴∠ANO=∠CMO.
在△ANO和△CMO中,
$\left\{\begin{array}{l}{∠ANO=∠CMO}\\{∠AON=∠COM}\\{AO=OC}\end{array}\right.$,
∴△ANO≌△CMO.
∴AN=MC.
∴AM=AN.
∴△AMN是等腰三角形.
点评 本题主要考查的是翻折的性质、全等三角形的性质和判定,证得△ANO≌△CMO是解题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
16.在Rt△ABC中,已知∠B=90°,AC=10,AB=5$\sqrt{2}$,则∠A等于( )
| A. | 45° | B. | 30° | C. | 60° | D. | 50° |
20.下列不等式中,是一元一次不等式的是( )
| A. | 2(1-y)+y>4y+2 | B. | x(x-5)≥4 | C. | $\frac{1}{2}-\frac{1}{4}>\frac{1}{5}$ | D. | y+1<y+2 |
1.在10张奖券中,有4张有奖,从中任抽一张,能中奖的概率为( )
| A. | $\frac{4}{10}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
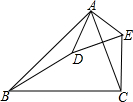 如图所示,△ABC∽△ADE.求证:
如图所示,△ABC∽△ADE.求证: 如图,△ABE和△ACD是△ABC分别沿着AB、AC边翻折180°形成的,若∠BAC=150°,求∠θ的度数.
如图,△ABE和△ACD是△ABC分别沿着AB、AC边翻折180°形成的,若∠BAC=150°,求∠θ的度数.