题目内容
9.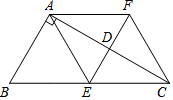 如图,在△ABC中,∠BAC=90°,线段AC的垂直平分线交AC于D点,交BC于E点,过点A作BC的平行线交直线ED于F点,连接AE,CF.
如图,在△ABC中,∠BAC=90°,线段AC的垂直平分线交AC于D点,交BC于E点,过点A作BC的平行线交直线ED于F点,连接AE,CF.(1)求证:四边形AECF是菱形;
(2)若AB=10,∠ACB=30°,求菱形AECF的面积.
分析 (1)只要证明AF=FC=CE=EA,即可判断四边形AECF是菱形;
(2)求出菱形的对角线的长,根据菱形的面积等于对角线乘积的一半计算即可;
解答 (1)证明:∵EF垂直平分AC,
∴FA=FC,EA=EC,
∵AF∥BC,
∴∠1=∠2.
∵AE=CE,
∴∠2=∠3.
∴∠1=∠3.
∵EF⊥AC,
∴∠ADF=∠ADE=90°.
∵∠1+∠4=90°,∠3+∠5=90°.
∴∠4=∠5.
∴AF=AE,
∴AF=FC=CE=EA,
∴四边形AECF是菱形.
(2)解:∵∠BAC=∠ADF=90°,
∴AB∥FE,
∵AF∥BE,
∴四边形ABEF为平行四边形,
∵AB=10,
∴FE=AB=10,
∵∠ACB=30°,
∴AC=$\frac{AB}{tan∠ACB}$=10$\sqrt{3}$,.
∴${S_{菱形AECF}}=\frac{1}{2}AC•FE=50\sqrt{3}$.
点评 本题考查菱形的判定和性质、相等的垂直平分线的性质、锐角三角函数等知识,解题的关键是熟练掌握菱形的判定,属于基础题,中考常考题型.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
20. 如图,四边形ABCD是菱形,E、F、G、H分别是各边的中点,随机向菱形ABCD内部掷一粒米,则米粒落到阴影区域内的概率是( )
如图,四边形ABCD是菱形,E、F、G、H分别是各边的中点,随机向菱形ABCD内部掷一粒米,则米粒落到阴影区域内的概率是( )
 如图,四边形ABCD是菱形,E、F、G、H分别是各边的中点,随机向菱形ABCD内部掷一粒米,则米粒落到阴影区域内的概率是( )
如图,四边形ABCD是菱形,E、F、G、H分别是各边的中点,随机向菱形ABCD内部掷一粒米,则米粒落到阴影区域内的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{8}$ | D. | $\frac{2}{3}$ |
1.某校甲、乙、丙、丁四名同学在运动会上参加4×100米接力比赛,其中甲跑第一棒,那么乙跑第二棒的概率为( )
| A. | $\frac{1}{24}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
 如图,四边形ABCD为正方形,点A、B在y轴上,点C的坐标为(-4,1),反比例函数y=$\frac{k}{x}$的图象经过点D,则k的值为12.
如图,四边形ABCD为正方形,点A、B在y轴上,点C的坐标为(-4,1),反比例函数y=$\frac{k}{x}$的图象经过点D,则k的值为12. 如图,AB为⊙O的直径,弦BC,DE相交于点F,且DE⊥AB于点G,过点C作⊙O的切线交DE的延长线于点H.
如图,AB为⊙O的直径,弦BC,DE相交于点F,且DE⊥AB于点G,过点C作⊙O的切线交DE的延长线于点H.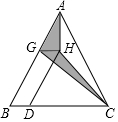 如图,△ABC的面积为16,点D是BC边上一点,且BD=$\frac{1}{4}$BC,点G是AB上一点,点B在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是4.
如图,△ABC的面积为16,点D是BC边上一点,且BD=$\frac{1}{4}$BC,点G是AB上一点,点B在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是4.
 如图所示,图中是某中学初一(1)班某次期中考试成绩各个分数段人数的统计图,已知其中不及格同学的人数占全班人数的$\frac{1}{13}$.
如图所示,图中是某中学初一(1)班某次期中考试成绩各个分数段人数的统计图,已知其中不及格同学的人数占全班人数的$\frac{1}{13}$.