题目内容
 如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.
如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.(1)若四边形AEDF的周长为24,AB=15,求AC的长;
(2)求证:EF垂直平分AD.
考点:直角三角形斜边上的中线,线段垂直平分线的性质
专题:
分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得DE=AE=
AB,DF=AF=
AC,然后求出AE+DE=AB,再求解即可;
(2)根据到线段两端点距离相等的点在线段的垂直平分线证明.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据到线段两端点距离相等的点在线段的垂直平分线证明.
解答:(1)解:∵AD是高,E、F分别是AB、AC的中点,
∴DE=AE=
AB,DF=AF=
AC,
∴AE+DE=AB=15,AF+DF=AC,
∵四边形AEDF的周长为24,AB=15,
∴AC=24-15=9;
(2)证明:∵DE=AE,DF=AF,
∴点E、F在线段AD的垂直平分线上,
∴EF垂直平分AD.
∴DE=AE=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE+DE=AB=15,AF+DF=AC,
∵四边形AEDF的周长为24,AB=15,
∴AC=24-15=9;
(2)证明:∵DE=AE,DF=AF,
∴点E、F在线段AD的垂直平分线上,
∴EF垂直平分AD.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,到线段两端点距离相等的点在线段的垂直平分线的性质,熟记性质是解题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 如图,已知A、B、C三点在⊙O上,∠A=50°,则∠BOC的度数为( )
如图,已知A、B、C三点在⊙O上,∠A=50°,则∠BOC的度数为( )| A、50° | B、25° |
| C、75° | D、100° |
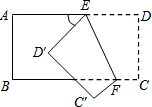 如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFB=65°,则∠AED′等于( )
如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFB=65°,则∠AED′等于( )| A、70° | B、65° |
| C、50° | D、25° |
 如图,直线a∥b,另一直线与a、b分别相交于点A、B,AE⊥b于E,若∠1=58°,则∠2=( )
如图,直线a∥b,另一直线与a、b分别相交于点A、B,AE⊥b于E,若∠1=58°,则∠2=( )| A、42° | B、58° |
| C、30° | D、32° |
目前全球海洋总面积约为36 106万平方公里,36106万用科学记数法表示为( )
| A、3.6106×108 |
| B、3.610 6×107 |
| C、3.6106×109 |
| D、36.106×107 |
 已知:如图,C,D是以线段AB为直径的⊙O上的两点,且四边形OBCD是菱形.求证:
已知:如图,C,D是以线段AB为直径的⊙O上的两点,且四边形OBCD是菱形.求证: