题目内容
 已知:如图,C,D是以线段AB为直径的⊙O上的两点,且四边形OBCD是菱形.求证:
已知:如图,C,D是以线段AB为直径的⊙O上的两点,且四边形OBCD是菱形.求证: |
| AD |
 |
| DC |
考点:圆心角、弧、弦的关系,菱形的性质
专题:证明题
分析:首先连接OC,由四边形OBCD是菱形,易得OB=OC=BC,则可证得∠2=∠3=∠B=∠1,则可得
=
.
 |
| AD |
 |
| DC |
解答: 证明:连结OC,
证明:连结OC,
∵四边形OBCD是菱形,
∴OB=BC,∠3=∠2,OD∥BC,
∴∠1=∠B,
又∵OC=OB=BC,
∴OC=BC,
∴∠3=∠B,
∴∠1=∠2,
∴
=
.
 证明:连结OC,
证明:连结OC,∵四边形OBCD是菱形,
∴OB=BC,∠3=∠2,OD∥BC,
∴∠1=∠B,
又∵OC=OB=BC,
∴OC=BC,
∴∠3=∠B,
∴∠1=∠2,
∴
 |
| AD |
 |
| DC |
点评:此题考查了圆心角与弧的关系以及菱形的性质.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
在平面直角坐标系中,点P(a,b)在第二象限,且|a|=3,b2=9,则P点坐标为( )
| A、(-3,18) |
| B、(-3,-3) |
| C、(-3,3) |
| D、(3,-3) |
 如图,⊙A,⊙B,⊙C两两不相交,且半径都是0.5,则图中阴影部分的面积是( )
如图,⊙A,⊙B,⊙C两两不相交,且半径都是0.5,则图中阴影部分的面积是( )| A、0.5π | B、0.25π |
| C、0.125π | D、2π |
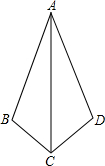 如图,∠BAC=∠DAC,∠B=∠D.求证:AB=AD.
如图,∠BAC=∠DAC,∠B=∠D.求证:AB=AD. 如图△ABC中,∠A=36°,AB=AC,且BD平分∠ABC交AC于点D,若AB=2,则AD=
如图△ABC中,∠A=36°,AB=AC,且BD平分∠ABC交AC于点D,若AB=2,则AD=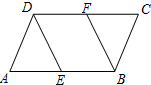 如图,在平行四边形ABCD中,AE=CF.求证:
如图,在平行四边形ABCD中,AE=CF.求证: 如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.
如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.