题目内容
解方程组:
.
|
考点:解三元一次方程组
专题:
分析:根据③×4+②得出4x+9y=96,再根据①得出4x=3y,再代入4x+9y=96中,求出y的值,再把y的值代入4x=3y中,求出x的值,再把x,y的值代入③,求出z的值,从而求出方程组的解.
解答:解:
,
③×4+②得:4x+9y=96 ④,
由①得:4x=3y ⑤,
把⑤代入④得:12y=96,
解得:y=8,
把y=8代入⑤得:x=6,
把x=6,y=8代入③得:z=10,
则原方程组的解为:
.
|
③×4+②得:4x+9y=96 ④,
由①得:4x=3y ⑤,
把⑤代入④得:12y=96,
解得:y=8,
把y=8代入⑤得:x=6,
把x=6,y=8代入③得:z=10,
则原方程组的解为:
|
点评:本题考查了三元一次方程组的解法,把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.

练习册系列答案
相关题目
 如图,把左边的图形折起来得到正方体,则下列正方体一定正确的是( )
如图,把左边的图形折起来得到正方体,则下列正方体一定正确的是( )A、 |
B、 |
C、 |
D、 |
 如图,某酒店为了吸引顾客,设立了一个可以自由转动的装盘,并规定:顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会,如果转盘停止后,若指针正好对准八折、七折、五折区域,顾客就可以获得此待遇(转盘分成12等份).
如图,某酒店为了吸引顾客,设立了一个可以自由转动的装盘,并规定:顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会,如果转盘停止后,若指针正好对准八折、七折、五折区域,顾客就可以获得此待遇(转盘分成12等份).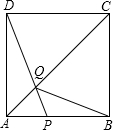 如图,在边长为6的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q,连接BQ,
如图,在边长为6的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q,连接BQ,