题目内容
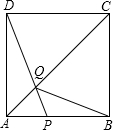 如图,在边长为6的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q,连接BQ,
如图,在边长为6的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q,连接BQ,(1)试证明:无论点P运动到AB上何处时,都有△ADQ≌△ABQ.
(2)当△ADQ的面积与正方形ABCD面积之比为1:6时,求BQ的长度.
(3)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P运动到什么位置时,AD=AQ(点P不与点A、C重合).
考点:正方形的性质,全等三角形的判定与性质,勾股定理
专题:动点型
分析:(1)根据正方形的四条边都相等可得AB=AD,对角线平分一组对角线可得∠DAC=∠BAC,然后利用“边角边”证明即可;
(2)过点Q作QE⊥AD于E,根据三角形的面积列式求出QE,再判断出△AEQ是等腰直角三角形,然后求出AE=EQ,再求出DE,然后利用勾股定理列式计算求出DQ,根据全等三角形对应边相等可得BQ=DQ;
(3)根据等边对等角可得∠ADQ=∠AQD,再根据两直线平行,内错角相等可得∠CPQ=∠ADQ,然后求出∠CQP=∠CPQ,再根据等角对等边可得CP=CQ.
(2)过点Q作QE⊥AD于E,根据三角形的面积列式求出QE,再判断出△AEQ是等腰直角三角形,然后求出AE=EQ,再求出DE,然后利用勾股定理列式计算求出DQ,根据全等三角形对应边相等可得BQ=DQ;
(3)根据等边对等角可得∠ADQ=∠AQD,再根据两直线平行,内错角相等可得∠CPQ=∠ADQ,然后求出∠CQP=∠CPQ,再根据等角对等边可得CP=CQ.
解答:(1)证明:在正方形ABCD中,AB=AD,∠DAC=∠BAC,
在△ADQ和△ABQ中,
,
∴△ADQ≌△ABQ(SAS);
(2)解:如图,过点Q作QE⊥AD于E,
∵△ADQ的面积与正方形ABCD面积之比为1:6,
∴S△ADQ=
×6QE=
×62,
解得QE=2,
∵∠DAC=
∠BAD=45°,
∴△AEQ是等腰直角三角形,
∴AE=EQ=2,
∴DE=AD-AE=6-2=4,
在Rt△DEQ中,DQ=
=
=2
,
∵△ADQ≌△ABQ,
∴BQ=DQ=2
;
(3)解:∵AD=AQ,
∴∠ADQ=∠AQD,
∵正方形的对边AD∥BC,
∴∠CPQ=∠ADQ,
又∵∠AQD=∠CQP(对顶角相等),
∴∠CQP=∠CPQ,
∴CP=CQ,
∵正方形ABCD的边长为6,
∴AC=6
,
∴CP=6
-6,
故当点P运动到距离点C6
-6时,AD=AQ.
在△ADQ和△ABQ中,
|
∴△ADQ≌△ABQ(SAS);
(2)解:如图,过点Q作QE⊥AD于E,
∵△ADQ的面积与正方形ABCD面积之比为1:6,
∴S△ADQ=
| 1 |
| 2 |
| 1 |
| 6 |

解得QE=2,
∵∠DAC=
| 1 |
| 2 |
∴△AEQ是等腰直角三角形,
∴AE=EQ=2,
∴DE=AD-AE=6-2=4,
在Rt△DEQ中,DQ=
| DE2+QE2 |
| 42+22 |
| 5 |
∵△ADQ≌△ABQ,
∴BQ=DQ=2
| 5 |
(3)解:∵AD=AQ,
∴∠ADQ=∠AQD,

∵正方形的对边AD∥BC,
∴∠CPQ=∠ADQ,
又∵∠AQD=∠CQP(对顶角相等),
∴∠CQP=∠CPQ,
∴CP=CQ,
∵正方形ABCD的边长为6,
∴AC=6
| 2 |
∴CP=6
| 2 |
故当点P运动到距离点C6
| 2 |
点评:本题考查了正方形的性质,全等三角形的判定与性质,勾股定理,等腰直角三角形的判定与性质,等边对等角和等角对等边的性质,熟记各性质是解题的关键.

练习册系列答案
相关题目
 如图,?ABCD中,∠B=70°,点E是BC的中点,点F在AB上,且BF=BE,过点F作FG⊥CD于点G,则∠EGC的度数为( )
如图,?ABCD中,∠B=70°,点E是BC的中点,点F在AB上,且BF=BE,过点F作FG⊥CD于点G,则∠EGC的度数为( )| A、35° | B、45° |
| C、30° | D、55° |
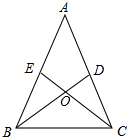 已知:如图,在锐角三角形ABC中,AB=AC,两条高BD与CE相交于点O,求证:OB=OC.
已知:如图,在锐角三角形ABC中,AB=AC,两条高BD与CE相交于点O,求证:OB=OC.
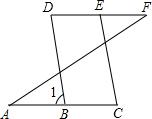 如图,已知:∠A=∠F,∠C=∠D,求证:BD∥EC,下面是不完整的说明过程,请将过程及其依据补充完整.
如图,已知:∠A=∠F,∠C=∠D,求证:BD∥EC,下面是不完整的说明过程,请将过程及其依据补充完整. 已知:如图,BE=CF,AB=DE,AC=DF,求证:△ABC≌△DEF.
已知:如图,BE=CF,AB=DE,AC=DF,求证:△ABC≌△DEF.