题目内容
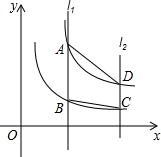 如图,平行于y轴的直线l1分别与双曲线y=
如图,平行于y轴的直线l1分别与双曲线y=| 4 |
| x |
| 1 |
| x |
考点:反比例函数综合题
专题:探究型
分析:设直线l1的解析式为y1=a,线l2的解析式为y2=b(b>a>0),由于直线l1分别与双曲线y=
(x>0)和双曲线y=
(x>0)交于A、B两点,直线l2分别与这两支双曲线交于D、C两点,故可用a、b分别表示出AB及CD的长,再根据AB=2CD即可得出a、b的关系式,根据梯形的面积公式求解即可.
| 4 |
| x |
| 1 |
| x |
解答:解:设直线l1的解析式为y1=a,线l2的解析式为y2=b(b>a>0),
∵直线l1分别与双曲线y=
(x>0)和双曲线y=
(x>0)交于A、B两点,直线l2分别与这两支双曲线交于D、C两点,
∴AB=
-
=
,CD=
-
=
,
∵AB=2CD,即
=
,
∴b=2a,
∵l1∥y轴,l2∥y轴,
∴l1∥l2,
∴S梯形ABCD=
(AB+CD)•(b-a)
=
(
+
)•(b-a)
=
•
•(b-a)
=
•
•a
=
.
故答案为:
.
∵直线l1分别与双曲线y=
| 4 |
| x |
| 1 |
| x |
∴AB=
| 4 |
| a |
| 1 |
| a |
| 3 |
| a |
| 4 |
| b |
| 1 |
| b |
| 3 |
| b |
∵AB=2CD,即
| 3 |
| a |
| 6 |
| b |
∴b=2a,
∵l1∥y轴,l2∥y轴,
∴l1∥l2,
∴S梯形ABCD=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| a |
| 3 |
| b |
=
| 1 |
| 2 |
| 3(a+b) |
| ab |
=
| 1 |
| 2 |
| 9a |
| 2a2 |
=
| 9 |
| 4 |
故答案为:
| 9 |
| 4 |
点评:本题考查的是反比例函数综合题,涉及到一次函数与反比例函数的交点及梯形的面积公式等知识,难度适中.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
两个分式A=
,B=
-
,(其中x≠±2,)则A和B的关系是( )
| 4 |
| x2-4 |
| 1 |
| x+2 |
| 1 |
| x-2 |
| A、A=B | B、AB=1 |
| C、A>B | D、A+B=0 |
已知反比例函数y=
(a≠0)的图象,在每一个象限内,y随x的增大而增大,则一次函数y=ax-a的图象不经过( )
| a |
| x |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过点(-2,0)和(x1,0),其中1<x<2,与y轴的正半轴的交点(0,2)的下方,下列结论正确的是( )
如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过点(-2,0)和(x1,0),其中1<x<2,与y轴的正半轴的交点(0,2)的下方,下列结论正确的是( )| A、abc<0 |
| B、9a+c>3b |
| C、a-b>0 |
| D、2a-b+1>0 |
 如图,在⊙O中,∠BOC=48°,则∠A=
如图,在⊙O中,∠BOC=48°,则∠A=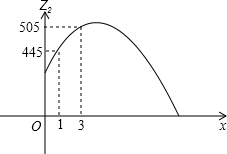 2012年国家商务部发布了商务预报监测,猪肉价格在1~3月下跌后,已跌至肉价的最低点;而重庆市菜价,却在上演一轮5元一把的藤藤菜、12元/千克的蘑菇、30元/千克的黑豆的涨价潮,“菜价高于肉价”让普通百姓表示吃不起素.进入3月,随着本地蔬菜的大量上市,我市蔬菜价格普遍下降.以下是重庆某一超市3月份每周的蘑菇销售价格变化如下表:
2012年国家商务部发布了商务预报监测,猪肉价格在1~3月下跌后,已跌至肉价的最低点;而重庆市菜价,却在上演一轮5元一把的藤藤菜、12元/千克的蘑菇、30元/千克的黑豆的涨价潮,“菜价高于肉价”让普通百姓表示吃不起素.进入3月,随着本地蔬菜的大量上市,我市蔬菜价格普遍下降.以下是重庆某一超市3月份每周的蘑菇销售价格变化如下表: 中央综治委在对全国各省市自治区2010年社会治安综合治理考评中,重庆市以93.48分居全国第一,成为全国最安全、最稳定的城市之一. 市政府非常重视交巡警平台的建设,据统计,某行政区在去年前7个月内,交巡警平台的数量与月份之间的关系如下表:
中央综治委在对全国各省市自治区2010年社会治安综合治理考评中,重庆市以93.48分居全国第一,成为全国最安全、最稳定的城市之一. 市政府非常重视交巡警平台的建设,据统计,某行政区在去年前7个月内,交巡警平台的数量与月份之间的关系如下表: