题目内容

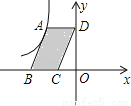
如图，点A是反比例函数y=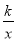（x＜0）的图象上的一点，过点A作平行四边形ABCD，使点B、C在x轴上，点D在y轴上．已知平行四边形ABCD的面积为6，则k的值为（　　）

A. 6 B. 3 C. ﹣6 D. ﹣3

C 【解析】作AE⊥BC于E，如图： ∵四边形ABCD为平行四边形， ∴AD∥x轴， ∴四边形ADOE为矩形， ∴S平行四边形ABCD=S矩形ADOE， 而S矩形ADOE=|?k|， ∴|?k|=6， 而k<0，即k<0， ∴k=?6. 故选：C.
练习册系列答案
相关题目

下列说法：?-a是负数；?-2的倒数是；?-（-3）的相反数是-3；④绝对值等于2的数2.其中正确的是（ ）

A. 1个 B. 2 个 C. 3个 D. 4个

B 【解析】因为a是不确定的数,所以?－a是负数错误,根据倒数的定义可得:－2的倒数是,所以?正确,根据相反数的定义, －（－3）的相反数是－3,所以?正确, 根据绝对值的定义,绝对值等于2的数是2和－2,所以④错误,故选B.

如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点．若⊙O的半径为7，则GE+FH的最大值为 ．

【解析】试题解析：当GH为⊙O的直径时，GE+FH有最大值． 当GH为直径时，E点与O点重合， ∴AC也是直径，AC=14． ∵∠ABC是直径上的圆周角， ∴∠ABC=90°， ∵∠C=30°， ∴AB=AC=7． ∵点E、F分别为AC、BC的中点， ∴EF=AB=3.5， ∴GE+FH=GH-EF=14-3.5=10.5．

选用适当的方法，解下列方程：（1）2x（x﹣2）=x﹣3；（2）（x﹣2）2=3x﹣6

（1） x=1或x=（2） x1=2，x2=5． 【解析】试题分析：（1）先化为一般式，再分解因式即可求解； （2）先移项后，提取公因式分解因式，即可求解. 试题解析：（1）2x（x﹣2）=x﹣3， 2x2﹣5x+3=0， （x-1）（2x-3）=0， x-1=0或2x-3=0， x=1或x=； （2）（x﹣2）2=3x﹣6， （x﹣2）2-3...

如图，线段AB与⊙O相切于点B，线段AO与⊙O相交于点C，AB=12，AC=8，则⊙O的半径长为　　．

A. 5 B. 6 C. 7 D. 8

A 【解析】连接OB， ∵AB切⊙O于B， ∴OB⊥AB， ∴∠ABO=90°， 设⊙O的半径长为r， 由勾股定理得：r2+122=(8+r)2， 解得r=5. 故选：A.

如图，在△ABC中，DE∥BC，∠ADE=∠EFC，AD：BD=5：3，CF=6，则DE的长为（ ）

A. 6 B. 8 C. 10 D. 12

C 【解析】∵DE∥BC， ∴∠ADE=∠B，∠AED=∠C， 又∵∠ADE=∠EFC， ∴∠B=∠EFC，△ADE∽△EFC， ∴BD∥EF，， ∴四边形BFED是平行四边形， ∴BD=EF， ∴，解得：DE=10. 故选C.

化简：.

【解析】 原式。 【解析】 试题分析：原式第一项利用完全平方公式化简，第二项利用单项式乘多项式法则计算，去括号合并即可得到结果。

背景资料:

在已知△ABC所在平面上求一点P，使它到三角形的三个顶点的距离之和最小．

这个问题是法国数学家费马1640年前后向意大利物理学家托里拆利提出的，所求的点被人们称为“费马点”．

如图①，当△ABC三个内角均小于120°时，费马点P在△ABC内部，此时∠APB＝∠BPC＝∠CPA＝120°，此时，PA＋PB＋PC的值最小．

解决问题：

（1）如图②，等边△ABC内有一点P，若点P到顶点A、B、C的距离分别为3，4，5，求∠APB的度数．

为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP′≌△ABP，这样就可以利用旋转变换，将三条线段PA，PB，PC转化到一个三角形中，从而求出∠APB=　 　；

基本运用：

（2）请你利用第（1）题的解答思想方法，解答下面问题：

如图③，△ABC中，∠CAB=90°，AB=AC，E，F为BC上的点，且∠EAF=45°，判断BE，EF，FC之间的数量关系并证明；

能力提升：

（3）如图④，在Rt△ABC中，∠C=90°，AC=1，∠ABC=30°，点P为Rt△ABC的费马点，

连接AP，BP，CP，求PA+PB+PC的值．

（1）150°； （2）E′F2=CE′2+FC2，理由见解析； （3）． 【解析】试题分析：（1） （2）首先把△ACE绕点A顺时针旋转90°，得到△ACE′．连接E′F，由旋转的性质得，AE′=AE，CE′=BE，∠CAE′=∠BAE，∠ACE′=∠B，∠EAE′=90°，然后再证明△EAF≌△E′AF可得E′F=EF，，再利用勾股定理可得结论； （3）将△AOB...

如果∠A的余角是26°，那么∠A的补角为_______．

116° 【解析】试题解析：∠A的余角是26°， ∠A的补角为: 故答案为：

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网