题目内容
11．
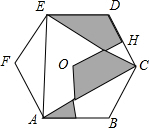如图，点O是正六边形ABCDEF的中心，OG⊥AB，垂足为G，OH⊥CD，垂足为H，若在正六边形所在区域内随机选取一点，则该点落在阴影区域内的概率为$\frac{1}{3}$．
分析 观察图形可知，△EOP的面积=△NOC的面积，△HPC的面积=△MNA的面积，可得阴影区域的面积是正六边形ABCDEF面积的$\frac{1}{3}$，根据几何概率即可求解．
解答 
解：如图，由图形可知，
△EOP的面积=△NOC的面积，△HPC的面积=△MNA的面积，
阴影区域的面积=正六边形ABCDEF面积的$\frac{1}{3}$，
则该点落在阴影区域内的概率为$\frac{1}{3}$．
故答案为：$\frac{1}{3}$．
点评 此题主要考查了几何概率问题，用到的知识点为：概率=相应的面积与总面积之比．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．如图，是中心对称图形但不是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
19．
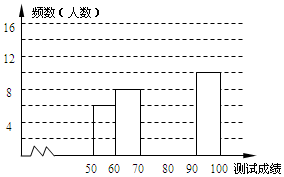“赏中华诗词，寻文化基因，品生活之美”，某校举办了首届“中国诗词大会”，经选拔后有50名学生参加决赛，这50名学生同时默写50首古诗词，若每正确默写出一首古诗词得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
请结合图表完成下列各题：
（1）①表中a的值为12，中位数在第3组；
②频数分布直方图补充完整；
（2）若测试成绩不低于80分为优秀，则本次测试的优秀率是多少？
（3）第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小明与小强两名男同学能分在同一组的概率．
“赏中华诗词，寻文化基因，品生活之美”，某校举办了首届“中国诗词大会”，经选拔后有50名学生参加决赛，这50名学生同时默写50首古诗词，若每正确默写出一首古诗词得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：请结合图表完成下列各题：
（1）①表中a的值为12，中位数在第3组；
②频数分布直方图补充完整；
（2）若测试成绩不低于80分为优秀，则本次测试的优秀率是多少？
（3）第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小明与小强两名男同学能分在同一组的概率．
| 组别 | 成绩x分 | 频数（人数） |
| 第1组 | 50≤x＜60 | 6 |
| 第2组 | 60≤x＜70 | 8 |
| 第3组 | 70≤x＜80 | 14 |
| 第4组 | 80≤x＜90 | a |
| 第5组 | 90≤x＜100 | 10 |
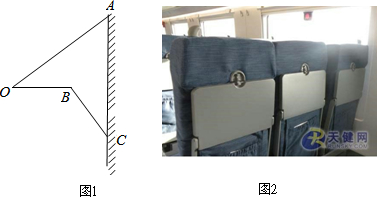
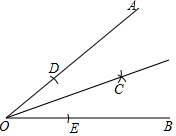如图所示，已知∠AOB=40°，现按照以下步骤作图：