题目内容
16.解方程:$\frac{x-4}{{x}^{2}-9}$+$\frac{1}{x+3}$=$\frac{2}{3-x}$.分析 分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:去分母得:x-4+x-3=-2x-6,
解得:x=$\frac{1}{4}$,
经检验x=$\frac{1}{4}$是分式方程的解.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.

练习册系列答案
相关题目
4.如图,在平面直角坐标系xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,每旋转60°为滚动1次,那么当正六边形ABCDEF滚动2017次时,点F的坐标是( )


| A. | (2017,0) | B. | (2017$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | C. | (2018,$\sqrt{3}$) | D. | (2018,0) |
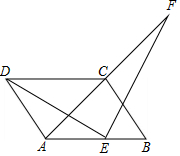 如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.
如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.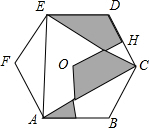 如图,点O是正六边形ABCDEF的中心,OG⊥AB,垂足为G,OH⊥CD,垂足为H,若在正六边形所在区域内随机选取一点,则该点落在阴影区域内的概率为$\frac{1}{3}$.
如图,点O是正六边形ABCDEF的中心,OG⊥AB,垂足为G,OH⊥CD,垂足为H,若在正六边形所在区域内随机选取一点,则该点落在阴影区域内的概率为$\frac{1}{3}$.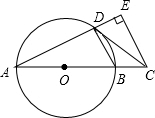 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
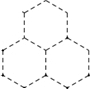 如图,是由大小完全相同的正六边形组成的图形,小军准备用红色、黄色、蓝色随机给每个正六边形分别涂上其中的一种颜色,则上方的正六边形涂红色的概率是$\frac{1}{3}$.
如图,是由大小完全相同的正六边形组成的图形,小军准备用红色、黄色、蓝色随机给每个正六边形分别涂上其中的一种颜色,则上方的正六边形涂红色的概率是$\frac{1}{3}$.