题目内容
6.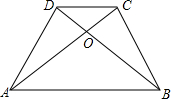 如图,已知在梯形ABCD中,AB∥CD,且AB=3CD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,那么$\overrightarrow{AO}$$\frac{1}{4}\overrightarrow{a}$+$\frac{3}{4}\overrightarrow{b}$(用$\overrightarrow{a}$,$\overrightarrow{b}$的式子表示)
如图,已知在梯形ABCD中,AB∥CD,且AB=3CD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,那么$\overrightarrow{AO}$$\frac{1}{4}\overrightarrow{a}$+$\frac{3}{4}\overrightarrow{b}$(用$\overrightarrow{a}$,$\overrightarrow{b}$的式子表示)
分析 由AB∥CD,且AB=3CD,可求得$\overrightarrow{DC}$,然后利用三角形法则求得$\overrightarrow{AC}$,再由AB∥CD,证得△AOB∽△COD,根据相似三角形的对应边成比例,求得答案.
解答 解:∵AB∥CD,且AB=3CD,
$\overrightarrow{BD}$=$\overrightarrow{b}-\overrightarrow{a}$
$\overrightarrow{BO}$=$\frac{3}{4}$($\overrightarrow{b}-\overrightarrow{a}$)
∴$\overrightarrow{AO}$=$\overrightarrow{a}+\overrightarrow{BO}$=$\frac{1}{4}\overrightarrow{a}+\frac{3}{4}\overrightarrow{b}$.
故答案为:$\frac{1}{4}\overrightarrow{a}+\frac{3}{4}\overrightarrow{b}$.
点评 此题考查了平面向量的知识与相似三角形的判定与性质.注意掌握三角形法则的应用.

练习册系列答案
相关题目
16.已知α、β是一元二次方程x2-2x-3=0的两个根,则α+β的值是( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
11. 如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )| A. | 美 | B. | 丽 | C. | 包 | D. | 头 |
18.在平面直角坐标系中,点P(-3,5)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
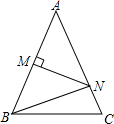 如图,△ABC中,AB=AC,∠A=38°,MN垂直平分AB,则∠BNC=76°.
如图,△ABC中,AB=AC,∠A=38°,MN垂直平分AB,则∠BNC=76°.