题目内容
定义[x]是指不超过x的最大整数,例如[1.3]=1,[0.9]=0.则函数y=
的x的取值范围是 ,y的取值范围是 .
| 1 |
| x-[x] |
考点:取整计算
专题:常规题型
分析:根据分式有意义分母不为零,结合定义[x]是指不超过x的最大整数,可得出x的范围,继而根据x-[x]的范围可得出y的范围.
解答:解:∵x-[x]≠0,
∴可得x不可为整数,
即x的范围为:x≠任何整数;
又∵[x]是指不超过x的最大整数,
∴0<x-[x]<1,
∴
>1,
即y的范围为:y>1.
故答案为:x≠任何整数、y>1.
∴可得x不可为整数,
即x的范围为:x≠任何整数;
又∵[x]是指不超过x的最大整数,
∴0<x-[x]<1,
∴
| 1 |
| x-[x] |
即y的范围为:y>1.
故答案为:x≠任何整数、y>1.
点评:此题考查了取整函数的知识,涉及了分式有意义的条件:分式有意义分母不为零,另外要仔细审题,理解[x]的意义.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
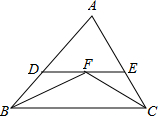 如图,△ABC中,DE∥BC,FB,FC分别平分∠B和∠C,已知BC=20,AB=18,AC=16,则△ADE的周长是( )
如图,△ABC中,DE∥BC,FB,FC分别平分∠B和∠C,已知BC=20,AB=18,AC=16,则△ADE的周长是( )| A、30 | B、32 | C、34 | D、36 |
 如图,在矩形ABCD中,AB=b,AD=a,过D和B作DE⊥AC,BF⊥AC,且AE=EF,试求a与b之间的关系.
如图,在矩形ABCD中,AB=b,AD=a,过D和B作DE⊥AC,BF⊥AC,且AE=EF,试求a与b之间的关系.