题目内容
9. 在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向B移动,点Q从点B开始以2cm/s的速度沿BC边向点C移点.
在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向B移动,点Q从点B开始以2cm/s的速度沿BC边向点C移点.(1)如果P,Q分别从A,B同时出发,点Q运动到点C时点Q、点P都停止运动,几秒后△PBQ的面积等于8cm2?
(2)如果P,Q分别从A,B同时出发,点Q运动到点C时点Q、点P都停止运动,是否存在某一时刻使得△PQD的面积等于8cm2?若存在,求出运动的时间;若不存在,说明理由.
(3)如果P,Q分别从A,B同时出发,当点Q运动到点D时,P、Q两点同时停止运动,试求△PQD的面积y与P、Q两个点运动时的时间x之间的函数关系式.
分析 (1)设x秒后△PBQ的面积等于8cm2,根据三角形面积公式列出方程,解方程得到答案;
(2)根据题意列出方程,应用一元二次方程根的判别式判断根的情况进行说明;
(3)根据矩形的性质和三角形面积公式列出函数关系式.
解答 解:(1)设x秒后△PBQ的面积等于8cm2,
PB=6-x,BQ=2x,
由题意得,$\frac{1}{2}$×(6-x)×2x=8,
解得x1=2,x2=4.
答:2秒或4秒后△PBQ的面积等于8cm2;
(2)y秒后△PQD的面积等于8cm2,
AP=y,PB=6-y,BQ=2y,CQ=12-2y,
6×12-$\frac{1}{2}$×y×12-$\frac{1}{2}$×(6-y)×2y-$\frac{1}{2}$×(12-2y)×6=8,
整理得y2-6y+28=0,
△=36-4×28<0,此方程无解,
∴不存在某一时刻使得△PQD的面积等于8cm2;
(3)由(2)得,
y=6×12-$\frac{1}{2}$×x×12-$\frac{1}{2}$×(6-x)×2x-$\frac{1}{2}$×(12-2x)×6
=x2-6x+36.
点评 本题考查的是矩形的性质、二次函数解析式的求法,根据矩形的性质列出函数解析式是解题的关键,注意一元二次方程根的判别式的应用.

练习册系列答案
相关题目
19.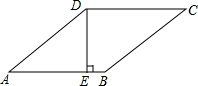 如图,在菱形ABCD中,DE⊥AB,垂足为E,DE=4,sinA=$\frac{2}{5}$,则菱形ABCD的周长是( )
如图,在菱形ABCD中,DE⊥AB,垂足为E,DE=4,sinA=$\frac{2}{5}$,则菱形ABCD的周长是( )
 如图,在菱形ABCD中,DE⊥AB,垂足为E,DE=4,sinA=$\frac{2}{5}$,则菱形ABCD的周长是( )
如图,在菱形ABCD中,DE⊥AB,垂足为E,DE=4,sinA=$\frac{2}{5}$,则菱形ABCD的周长是( )| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
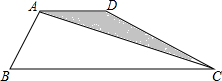 如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的面积是$\sqrt{3}$.
如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的面积是$\sqrt{3}$.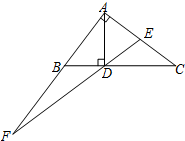 如图,△ABC中,∠BAC=90°,AD⊥BC于点D,点E为AC的中点,ED的延长线交AB的延长线于点F.若AB=5,BD=3,则$\frac{DF}{AF}$=$\frac{3}{4}$.
如图,△ABC中,∠BAC=90°,AD⊥BC于点D,点E为AC的中点,ED的延长线交AB的延长线于点F.若AB=5,BD=3,则$\frac{DF}{AF}$=$\frac{3}{4}$.