题目内容
1.已知|5-2x|+(5-y)2=0,x,y分别是方程ax-1=0和2y-b+1=0的解,求代数式(5a-4)2011(b-10$\frac{1}{2}$)2012的值.分析 先根据非负数的性质求出x、y的值,再代入方程ax-1=0和2y-b+1=0求出a、b的值,代入代数式进行计算即可.
解答 解:∵|5-2x|+(5-y)2=0,
∴5-2x=0,5-y=0,解得x=$\frac{5}{2}$,y=5.
∵x,y分别是方程ax-1=0和2y-b+1=0的解,
∴$\frac{5}{2}$a-1=0,10-b+1=0,解得a=$\frac{2}{5}$,b=11,
∴原式=(2-4)2011(11-10$\frac{1}{2}$)2012=(-2)2011•($\frac{1}{2}$)2012=(-2×$\frac{1}{2}$)2011×$\frac{1}{2}$=-$\frac{1}{2}$.
点评 本题考查的是二元一次方程的解,熟知非负数的性质及有理数乘方的法则是解答此题的关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
16.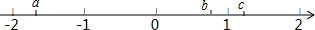 已知有理数a,b,c在数轴上的位置如图,则在-$\frac{1}{a}$,-a,c-b,c+a中,最小的一个是( )
已知有理数a,b,c在数轴上的位置如图,则在-$\frac{1}{a}$,-a,c-b,c+a中,最小的一个是( )
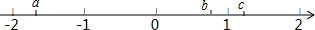 已知有理数a,b,c在数轴上的位置如图,则在-$\frac{1}{a}$,-a,c-b,c+a中,最小的一个是( )
已知有理数a,b,c在数轴上的位置如图,则在-$\frac{1}{a}$,-a,c-b,c+a中,最小的一个是( )| A. | -a | B. | c-b | C. | c+a | D. | -$\frac{1}{a}$ |
 如图,正方形ABCD的顶点A、B和正方形EFGH的顶点G、H在一个半径为5cm的⊙O上,点E、F在线段CD上,正方形ABCD的边长为6cm,则正方形正方形EFGH的边长为2.8cm.
如图,正方形ABCD的顶点A、B和正方形EFGH的顶点G、H在一个半径为5cm的⊙O上,点E、F在线段CD上,正方形ABCD的边长为6cm,则正方形正方形EFGH的边长为2.8cm. 在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向B移动,点Q从点B开始以2cm/s的速度沿BC边向点C移点.
在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向B移动,点Q从点B开始以2cm/s的速度沿BC边向点C移点.