题目内容
14.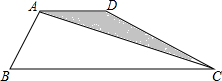 如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的面积是$\sqrt{3}$.
如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的面积是$\sqrt{3}$.
分析 如图,过点A作AE⊥BC于E,过点D作DF⊥BC于F.构建矩形AEFD和直角三角形,通过含30度角的直角三角形的性质求得AE的长度,然后由三角形的面积公式进行解答即可.
解答 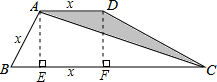 解:如图,过点A作AE⊥BC于E,过点D作DF⊥BC于F.设AB=AD=x.
解:如图,过点A作AE⊥BC于E,过点D作DF⊥BC于F.设AB=AD=x.
又∵AD∥BC,
∴四边形AEFD是矩形形,
∴AD=EF=x.
在Rt△ABE中,∠ABC=60°,则∠BAE=30°,
∴BE=$\frac{1}{2}$AB=$\frac{1}{2}$x,
∴DF=AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\frac{\sqrt{3}}{2}$x,
在Rt△CDF中,∠FCD=30°,则CF=DF•cot30°=$\frac{3}{2}$x.
又∵BC=6,
∴BE+EF+CF=6,即$\frac{1}{2}$x+x+$\frac{3}{2}$x=6,
解得 x=2
∴△ACD的面积是:$\frac{1}{2}$AD•DF=$\frac{1}{2}$x×$\frac{\sqrt{3}}{2}$x=$\frac{\sqrt{3}}{4}$×22=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查了勾股定理,三角形的面积以及含30度角的直角三角形.解题的难点是作出辅助线,构建矩形和直角三角形,目的是求得△ADC的底边AD以及该边上的高线DF的长度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.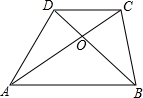 如图,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O,有下面四个结论:①△AOB∽△COD;②△AOD∽△BOC;③S△AOD=S△BOC;④S△DOC:S△BOA=DC:AB,其中,结论一定正确的有( )
如图,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O,有下面四个结论:①△AOB∽△COD;②△AOD∽△BOC;③S△AOD=S△BOC;④S△DOC:S△BOA=DC:AB,其中,结论一定正确的有( )
 如图,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O,有下面四个结论:①△AOB∽△COD;②△AOD∽△BOC;③S△AOD=S△BOC;④S△DOC:S△BOA=DC:AB,其中,结论一定正确的有( )
如图,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O,有下面四个结论:①△AOB∽△COD;②△AOD∽△BOC;③S△AOD=S△BOC;④S△DOC:S△BOA=DC:AB,其中,结论一定正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.若$\sqrt{(a-b)^{2}}$=b-a,则( )
| A. | a>b | B. | a<b | C. | a≥b | D. | a≤b |
2.多项式36a3b2-18a2b3+12a2b2各项的公因式是( )
| A. | a2b2 | B. | 12a3b3 | C. | 6a3b3 | D. | 6a2b2 |
 在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向B移动,点Q从点B开始以2cm/s的速度沿BC边向点C移点.
在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向B移动,点Q从点B开始以2cm/s的速度沿BC边向点C移点.
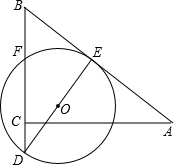 如图,△ABC中,AC=4,BC=3,∠ACB=90°,E、F分别为AB、BC的中点,⊙O经过E、F两点,点C在⊙O内,延长BC交⊙O于D.若∠BDO=∠A.
如图,△ABC中,AC=4,BC=3,∠ACB=90°,E、F分别为AB、BC的中点,⊙O经过E、F两点,点C在⊙O内,延长BC交⊙O于D.若∠BDO=∠A.