题目内容
5.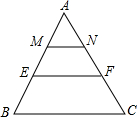 如图,在△ABC中,M,E把AB边三等分,MN∥EF∥BC,则△AMN,四边形MEFN,四边形EBCF的面积比为( )
如图,在△ABC中,M,E把AB边三等分,MN∥EF∥BC,则△AMN,四边形MEFN,四边形EBCF的面积比为( )| A. | 1:1:1 | B. | 1:2:3 | C. | 1:4:9 | D. | 1:3:5 |
分析 根据平行线等分线段定理可以推出N、F也把AC边三等分,根据已知条件可以得出△AMN∽△AEF∽△ABC,所以其相似比为1:2:3,然后根据三角形的面积比为相似比的平方,即可得出自上而下三部分的面积比.
解答 解:∵在△ABC中,M、E把AB边三等分,MN∥EF∥BC
∴N、F两点把AC三等分
∴∠AMN=∠AEF=∠ABC,∠ANM=∠AFE=∠ACB
∵∠A=∠A
∴△AMN∽△AEF∽△ABC
∴AM:AE:AB=1:2:3
∴S△AMN:S△AEF:S△ABC=1:4:9
∴△AMN,四边形MEFN,四边形EBCF的面积比为:1:3:5
故选D.
点评 本题重点考查相似三角形的判定定理和性质,平行线等分线段定理,关键是求出相似三角形的相似比.

练习册系列答案
相关题目
15.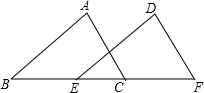 如图,B,C,E,F四点在一条直线上,下列条件能判定△ABC与△DEF全等的是( )
如图,B,C,E,F四点在一条直线上,下列条件能判定△ABC与△DEF全等的是( )
 如图,B,C,E,F四点在一条直线上,下列条件能判定△ABC与△DEF全等的是( )
如图,B,C,E,F四点在一条直线上,下列条件能判定△ABC与△DEF全等的是( )| A. | AB∥DE,∠A=∠D,BE=CF | B. | AB∥DE,AB=DE,AC=DF | ||
| C. | AB∥DE,AC=DF,BE=CF | D. | AB∥DE,AC∥DF,∠A=∠D |
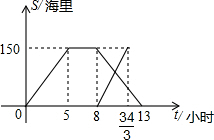 黄岩岛是我国南沙群岛的一个小岛,一天某渔船在该海域捕鱼,突然发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告并立即返航,渔政船接到报告后,立即出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t的函数图象.(假设渔船和渔政船沿同一航线航行)则在渔政船驶往黄岩岛的过程中,渔船从港口出发经过9.6或10.4小时与渔政船相距30海里.
黄岩岛是我国南沙群岛的一个小岛,一天某渔船在该海域捕鱼,突然发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告并立即返航,渔政船接到报告后,立即出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t的函数图象.(假设渔船和渔政船沿同一航线航行)则在渔政船驶往黄岩岛的过程中,渔船从港口出发经过9.6或10.4小时与渔政船相距30海里. 如图:E是平行四边形AD边上的一点,连接CE,并延长CE与BA的延长线交于点F,已知CE=ED,∠F=80°,求平行四边形各内角大小.
如图:E是平行四边形AD边上的一点,连接CE,并延长CE与BA的延长线交于点F,已知CE=ED,∠F=80°,求平行四边形各内角大小.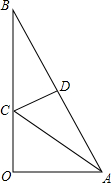 如图,直角三角形纸片OAB,∠AOB=90°,OA=1,OB=2,折叠该纸片,折痕与边OB交于点C,与边AB交于点D,折叠后点B与点A重合.
如图,直角三角形纸片OAB,∠AOB=90°,OA=1,OB=2,折叠该纸片,折痕与边OB交于点C,与边AB交于点D,折叠后点B与点A重合.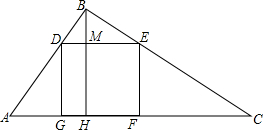 如图,有一块直角三角形木板ABC,面积为1.5m2,一条直角边AB为1.5m,现在要把它按图示加工成一个正方形桌面DEFG.
如图,有一块直角三角形木板ABC,面积为1.5m2,一条直角边AB为1.5m,现在要把它按图示加工成一个正方形桌面DEFG. 小明在楼顶A处测得对面大楼楼顶点C处的仰角为30°,在楼底点B处的仰角为60°.若两座楼AB与CD相距60米,则楼AB的高度约为40$\sqrt{3}$米.(结果保留根号)
小明在楼顶A处测得对面大楼楼顶点C处的仰角为30°,在楼底点B处的仰角为60°.若两座楼AB与CD相距60米,则楼AB的高度约为40$\sqrt{3}$米.(结果保留根号) 由一个英文单词由五个字母组成,分别对应如图中的有序数对,顺次为(5,3),(6,3),(7,3),(4,1),(4,4),请你把这个英文单词写出来并翻译成中文为study,“学习”.
由一个英文单词由五个字母组成,分别对应如图中的有序数对,顺次为(5,3),(6,3),(7,3),(4,1),(4,4),请你把这个英文单词写出来并翻译成中文为study,“学习”.