题目内容
17. 小明在楼顶A处测得对面大楼楼顶点C处的仰角为30°,在楼底点B处的仰角为60°.若两座楼AB与CD相距60米,则楼AB的高度约为40$\sqrt{3}$米.(结果保留根号)
小明在楼顶A处测得对面大楼楼顶点C处的仰角为30°,在楼底点B处的仰角为60°.若两座楼AB与CD相距60米,则楼AB的高度约为40$\sqrt{3}$米.(结果保留根号)
分析 根据三角函数求出CE和DC的长,相减即可得到CE的长.
解答  解:如图:在Rt△AEC中,CE=AE•tan30°=60×$\frac{\sqrt{3}}{3}$=20$\sqrt{3}$米;
解:如图:在Rt△AEC中,CE=AE•tan30°=60×$\frac{\sqrt{3}}{3}$=20$\sqrt{3}$米;
在Rt△AEC中,CD=BD•tan60°=60×$\sqrt{3}$=60$\sqrt{3}$米;
∴AB=60$\sqrt{3}$-20$\sqrt{3}$=40$\sqrt{3}$米.
故答案为40$\sqrt{3}$米.
点评 本题考查了解直角三角形的应用,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
8.淮北市富强文体平价店以每件50元的价格购进800件某体育用品,第一个月以单价80元销售,售出了200件,第二个月如果单价不变,预计仍可售出200件,为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,将对剩余的体育用品一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.
(1)填表:(不需化简)
(2)如果该店希望通过销售这批体育用品获利9000元,那么第二个月的单价应是多少元?
(1)填表:(不需化简)
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | 80-x | 40 |
| 销售量(件) | 200 | 200+10x | 400-10x |
5.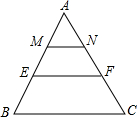 如图,在△ABC中,M,E把AB边三等分,MN∥EF∥BC,则△AMN,四边形MEFN,四边形EBCF的面积比为( )
如图,在△ABC中,M,E把AB边三等分,MN∥EF∥BC,则△AMN,四边形MEFN,四边形EBCF的面积比为( )
 如图,在△ABC中,M,E把AB边三等分,MN∥EF∥BC,则△AMN,四边形MEFN,四边形EBCF的面积比为( )
如图,在△ABC中,M,E把AB边三等分,MN∥EF∥BC,则△AMN,四边形MEFN,四边形EBCF的面积比为( )| A. | 1:1:1 | B. | 1:2:3 | C. | 1:4:9 | D. | 1:3:5 |
7.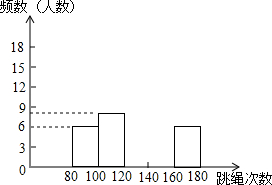 为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:
为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:
请结合图表完成下列问题:
(1)求表中的a;
(2)请把频数分布直方图补充完整;
(3)若七年级学生一分钟跳绳次数(x)达标要求是:80≤x<120不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.为使合格率达到90%,至少还要将几人跳绳水平从不合格提高到合格或合格以上?
 为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:
为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:| 组 别 | 次 数x | 频数(人数) |
| 第一组 | 80≤x<100 | 6 |
| 第二组 | 100≤x<120 | 8 |
| 第三组 | 120≤x<140 | a |
| 第四组 | 140≤x<160 | 18 |
| 第五组 | 160≤x<180 | 6 |
(1)求表中的a;
(2)请把频数分布直方图补充完整;
(3)若七年级学生一分钟跳绳次数(x)达标要求是:80≤x<120不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.为使合格率达到90%,至少还要将几人跳绳水平从不合格提高到合格或合格以上?
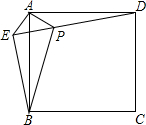 如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于P,若AE=AP=1,PB=$\sqrt{5}$;
如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于P,若AE=AP=1,PB=$\sqrt{5}$;