题目内容
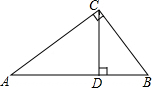 如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=6
如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=6| 3 |
| 3 |
考点:射影定理,勾股定理
专题:计算题
分析:先根据射影定理得到BC2=BD•BA,即(4
)2=BD•(BD+6
),解得BD=2
,然后在Rt△ACB中,利用含30度的直角三角形三边的关系可得到∠A的度数和AC的长.
| 3 |
| 3 |
| 3 |
解答:解:∵∠ACB=90°,CD⊥AB于点D,
∴BC2=BD•BA,
即(4
)2=BD•(BD+6
),
整理为BD2+6
BD-48=0,解得BD=2
或BD=-8
(舍去),
在Rt△ACB中,∵BC=4
,AB=AD+BD=8
,
∴∠A=30°,
AC=
BC=12.
∴BC2=BD•BA,
即(4
| 3 |
| 3 |
整理为BD2+6
| 3 |
| 3 |
| 3 |
在Rt△ACB中,∵BC=4
| 3 |
| 3 |
∴∠A=30°,
AC=
| 3 |
点评:本题考查了射影定理:直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项.每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.

练习册系列答案
相关题目
一个不透明的袋中装有除颜色外其余均相同的5个红球和3个黄球,若从中随机摸出一个,则摸到黄球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
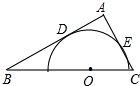 如图,已知△ABC是直角三角形,∠A=90°,AC=3,AB=4,O是BC上的点,⊙O与AB、AC相切于点D、E,求AD的长.
如图,已知△ABC是直角三角形,∠A=90°,AC=3,AB=4,O是BC上的点,⊙O与AB、AC相切于点D、E,求AD的长.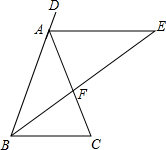 如图所示,在等腰△ABC中,AB=AC,∠BAC=36°,AE是△ABC的外角∠DAC的平分线,BF是∠ABC的平分线,BF的延长线交AE于E.
如图所示,在等腰△ABC中,AB=AC,∠BAC=36°,AE是△ABC的外角∠DAC的平分线,BF是∠ABC的平分线,BF的延长线交AE于E.