题目内容
已知平角AOB及其平分线OC,如果作射线OD,使∠BOD与∠COD的度数之比为7:3,那么∠AOD等于多少度?
考点:角平分线的定义
专题:
分析:根据题意画出图形,由角平分线的定义得出∠COB的度数,再根据∠BOD与∠COD的度数之比为7:3求出∠COD的度数,根据∠AOD=∠AOC+∠COD即可得出结论.
解答: 解:如图1所示,
解:如图1所示,
∵∠AOB=180°,OC是∠AOB的平分线,
∴∠COB=
×180°=90°.
∵∠BOD与∠COD的度数之比为7:3,
∴∠COD=
∠COB=
×90°=27°,
∴∠AOD=∠AOC+∠COD=90°+27°=117°.
如图2所示,∵∠AOD:∠COD=1:3,
∴∠AOD=90°×
=22.5°.
答:∠AOD等于117°或22.5°.
 解:如图1所示,
解:如图1所示,∵∠AOB=180°,OC是∠AOB的平分线,
∴∠COB=
| 1 |
| 2 |
∵∠BOD与∠COD的度数之比为7:3,
∴∠COD=
| 3 |
| 10 |
| 3 |
| 10 |
∴∠AOD=∠AOC+∠COD=90°+27°=117°.
如图2所示,∵∠AOD:∠COD=1:3,
∴∠AOD=90°×
| 1 |
| 4 |
答:∠AOD等于117°或22.5°.
点评:本题考查的是角平分线的定义,熟知从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解答此题的关键.

练习册系列答案
相关题目
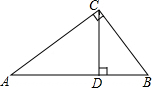 如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=6
如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=6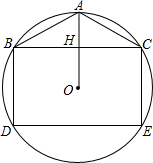 已知,如图,矩形BCED的两个顶点在⊙O上,过O作BC的垂线交BC于H,交⊙O于A,连AB,AC.
已知,如图,矩形BCED的两个顶点在⊙O上,过O作BC的垂线交BC于H,交⊙O于A,连AB,AC.