题目内容
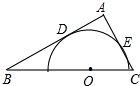如图，已知△ABC是直角三角形，∠A=90°，AC=3，AB=4，O是BC上的点，⊙O与AB、AC相切于点D、E，求AD的长．考点：切线的性质
专题：计算题
分析：连结OD、OE，如图，根据切线的性质得到OD⊥AB，OE⊥AC，则可判断四边形ADOE为矩形，加上OD=OE，于是可判断四边形ADOE为正方形，得到AD=AE=OE，设AD=x，则OE=x，AE=x，然后证明△COE∽△CBA，根据相似的性质得到
=
，再解方程即可．
| x |
| 4 |
| 3-x |
| 3 |
解答：解：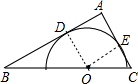
连结OD、OE，如图，
∵⊙O与AB、AC相切于点D、E，
∴OD⊥AB，OE⊥AC，
而∠A=90°，
∴四边形ADOE为矩形，
而OD=OE，
∴四边形ADOE为正方形，
∴AD=AE=OE，
设AD=x，则OE=x，AE=x，
∵OE∥AB，
∴△COE∽△CBA，
∴
=
，即
=
，解得x=
，
即AD的长为
．
连结OD、OE，如图，∵⊙O与AB、AC相切于点D、E，
∴OD⊥AB，OE⊥AC，
而∠A=90°，
∴四边形ADOE为矩形，
而OD=OE，
∴四边形ADOE为正方形，
∴AD=AE=OE，
设AD=x，则OE=x，AE=x，
∵OE∥AB，
∴△COE∽△CBA，
∴
| OE |
| AB |
| CE |
| CA |
| x |
| 4 |
| 3-x |
| 3 |
| 12 |
| 7 |
即AD的长为
| 12 |
| 7 |
点评：本题考查了切线的性质：①圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．也考查了相似三角形的判定与性质．
练习册系列答案
阅读快车系列答案
相关题目
在实数
，-
，-3.14，0，π，2.161 161 161…，
中，无理数有（ ）
| 1 |
| 2 |
| 3 |
| 3 | 16 |
| A、1 个 | B、2个 |
| C、3个 | D、4个 |
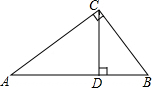如图所示，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，AD=6