题目内容
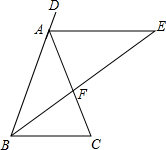如图所示，在等腰△ABC中，AB=AC，∠BAC=36°，AE是△ABC的外角∠DAC的平分线，BF是∠ABC的平分线，BF的延长线交AE于E．（1）求证：AF=FB=BC；
（2）求证：
| EF |
| BF |
| BC |
| FC |
考点：相似三角形的判定与性质,等腰三角形的性质
专题：证明题
分析：（1）由条件可求得∠FBA=BAC=∠FBC=36°，∠BFC=∠BCF=72°，可得AF=FB=BC；
（2）由条件可证明AE∥BC，则可得
=
，结合（1）AF=BC，代入可证得结论．
（2）由条件可证明AE∥BC，则可得
| EF |
| BF |
| AF |
| FC |
解答：证明：（1）∵AB=AC，∠BAC=36°，
∴∠ABC=∠ACB=72°，
∵BF平分∠ABC，
∴∠ABF=∠FBC=36°，
∴∠ABF=∠BAC，
∴AF=BF，
又∠BFC=∠BAF+∠FBA=72°=∠ACB，
∴BF=BC，
∴AF=FB=BC；
（2）∵∠BAC=36°，
∴∠DAC=144°，
∵AE平分∠DAC，
∴∠EAF=72°=∠ACB，
∴AE∥BC，
∴
=
，
∵AF=BC，
∴
=
．
∴∠ABC=∠ACB=72°，
∵BF平分∠ABC，
∴∠ABF=∠FBC=36°，
∴∠ABF=∠BAC，
∴AF=BF，
又∠BFC=∠BAF+∠FBA=72°=∠ACB，
∴BF=BC，
∴AF=FB=BC；
（2）∵∠BAC=36°，
∴∠DAC=144°，
∵AE平分∠DAC，
∴∠EAF=72°=∠ACB，
∴AE∥BC，
∴
| EF |
| BF |
| AF |
| FC |
∵AF=BC，
∴
| EF |
| BF |
| BC |
| FC |
点评：本题主要考查等腰三角形的判定和性质及平行线分线段成比例，掌握等角对等边是解题的关键，注意三角形内角和定理的灵活运用．
练习册系列答案
相关题目
下列近似数中，有四个有效数字的数是（ ）
| A、0.03 |
| B、0.04060 |
| C、0.00503 |
| D、0.0320 |
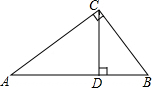如图所示，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，AD=6
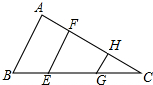如图，AB∥EF∥GH，BE=CG，求证：AB=EF+GH．
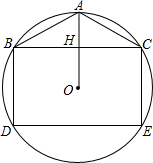已知，如图，矩形BCED的两个顶点在⊙O上，过O作BC的垂线交BC于H，交⊙O于A，连AB，AC．