题目内容
已知AD是△ABC外角∠EAC的平分线，求证：AB：AC=BD：DC．
考点：平行线分线段成比例
专题：证明题
分析：作DF∥AC交AE于F，如图，由AD是△ABC外角∠EAC的平分线得到∠1=∠2，由AC∥DF得∠2=∠3，则∠1=∠3，所以FA=FD，再根据平行线分线段成比例，
由AC∥DF得到AC：DF=BC：BD，AB：AF=BC：CD，利用比例的性质得到AC•BD=DF•BC，AB•CD=AF•BC，所以AC•BD=AB•CD，然后根据比例性质即可得到结论．
由AC∥DF得到AC：DF=BC：BD，AB：AF=BC：CD，利用比例的性质得到AC•BD=DF•BC，AB•CD=AF•BC，所以AC•BD=AB•CD，然后根据比例性质即可得到结论．
解答：证明：作DF∥AC交AE于F，如图，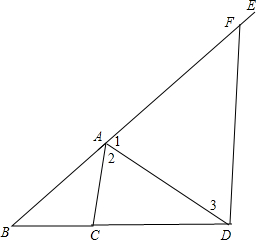
∵AD是△ABC外角∠EAC的平分线，
∴∠1=∠2，
∵AC∥DF，
∴∠2=∠3，
∴∠1=∠3，
∴FA=FD，
∵AC∥DF，
∴AC：DF=BC：BD，AB：AF=BC：CD，
∴AC•BD=DF•BC，AB•CD=AF•BC，
而FA=FD，
∴AC•BD=AB•CD，
∴AB：AC=BD：DC．
∵AD是△ABC外角∠EAC的平分线，
∴∠1=∠2，
∵AC∥DF，
∴∠2=∠3，
∴∠1=∠3，
∴FA=FD，
∵AC∥DF，
∴AC：DF=BC：BD，AB：AF=BC：CD，
∴AC•BD=DF•BC，AB•CD=AF•BC，
而FA=FD，
∴AC•BD=AB•CD，
∴AB：AC=BD：DC．
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．
练习册系列答案
名校课堂系列答案
相关题目
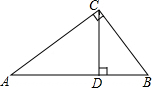如图所示，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，AD=6
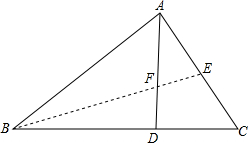如图，已知在△ABC中，D是BC上的一点，且BA2=BD•BC．
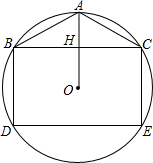已知，如图，矩形BCED的两个顶点在⊙O上，过O作BC的垂线交BC于H，交⊙O于A，连AB，AC．