题目内容
19. 如图所示,直线a经过正方形ABCD的顶点A,分别过此正方形的顶点B、D作BF⊥a于点F、DE⊥a于点E,若DE=3,BF=2,则正方形ABCD的面积为13.
如图所示,直线a经过正方形ABCD的顶点A,分别过此正方形的顶点B、D作BF⊥a于点F、DE⊥a于点E,若DE=3,BF=2,则正方形ABCD的面积为13.
分析 通过证明△ABF≌△DAE,得AF=DE,AE=BF,进而求出AB和EF,根据勾股定理即可得出正方形的面积.
解答 解:∵四边形ABCD是正方形,
∴AD=AB,
∵∠EAD+∠EDA=90°,且∠EAD+∠FAB=90°,
∴∠EDA=∠FAB,
在△ABE和△ADF中
$\left\{\begin{array}{l}{∠AED=∠AFB}\\{∠EDA=∠FAB}\\{AD=AB}\end{array}\right.$
∴△ABF≌△DAE(AAS),
即AF=DE=3,AE=BF=2,
∴AB=$\sqrt{A{F}^{2}+B{F}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
故正方形的面积为:($\sqrt{13}$)2=13,
故答案为13.
点评 本题考查了正方形的性质以及全等三角形的判定和勾股定理等知识,解本题的关键是证明△ABF≌△DAE.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.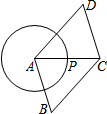 如图,点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=$\sqrt{3}$,则平行四边形ABCD面积的最大值为( )
如图,点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=$\sqrt{3}$,则平行四边形ABCD面积的最大值为( )
 如图,点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=$\sqrt{3}$,则平行四边形ABCD面积的最大值为( )
如图,点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=$\sqrt{3}$,则平行四边形ABCD面积的最大值为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 3 | D. | 3$\sqrt{3}$ |
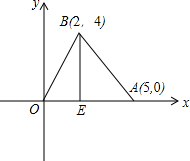 如图,在平面直角坐标系中,A(5,0),B(2,4),AB=5,BE垂直于x轴,垂足为点E,动点P从点A出发以3个单位/s的速度沿射线AB运动,动点Q从点O出发,在折线OA-AB上运动,在线段OA上以每秒5个单位速度运动,在AB上以每秒3个单位的速度,运动时间为t秒,若P、Q同时出发,点Q停止,点P随之停止运动.
如图,在平面直角坐标系中,A(5,0),B(2,4),AB=5,BE垂直于x轴,垂足为点E,动点P从点A出发以3个单位/s的速度沿射线AB运动,动点Q从点O出发,在折线OA-AB上运动,在线段OA上以每秒5个单位速度运动,在AB上以每秒3个单位的速度,运动时间为t秒,若P、Q同时出发,点Q停止,点P随之停止运动.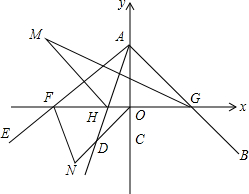 如图,平面直角坐标系中,∠BAC=45°,AC在y轴上,∠DAE=35°,AE,AB,AD分别交x轴于点F、G、H.在∠DAE旋转过程中,设AE交x轴于F,∠AGH的平分线与∠AHF的平分线交于点M,∠COF的平分线与∠OFE的平分线交于点N.下列两个结论:①∠N+∠M为定值;②∠N-∠M为定值.其中有且仅有一个是正确的,请你选出正确的结论,并求出其值.
如图,平面直角坐标系中,∠BAC=45°,AC在y轴上,∠DAE=35°,AE,AB,AD分别交x轴于点F、G、H.在∠DAE旋转过程中,设AE交x轴于F,∠AGH的平分线与∠AHF的平分线交于点M,∠COF的平分线与∠OFE的平分线交于点N.下列两个结论:①∠N+∠M为定值;②∠N-∠M为定值.其中有且仅有一个是正确的,请你选出正确的结论,并求出其值.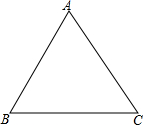 已知△ABC中,AB=AC=BC=3.请在图中用尺规作图画出△ABC的内切圆,保留作图痕迹,并求出内切圆的半径.
已知△ABC中,AB=AC=BC=3.请在图中用尺规作图画出△ABC的内切圆,保留作图痕迹,并求出内切圆的半径.