题目内容
16．
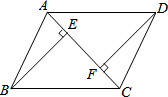如图，AB=CD，AF=CE，BE⊥AC于E，DF⊥AC于F．求证：（1）△ABE≌△CDF．
（2）AD∥BC．
分析 （1）首先证明AE=CF，然后根据HL即可证得；
（2）首先证明△ADF≌△CBE，根据全等三角形的对应角相等，即可证明∠DAF=∠BCE，根据平行线的性质证明．
解答 证明：（1）∵AF=CE，
∴AE=CF，
又∵BE⊥AC于E，DF⊥AC于F，
∴直角△ABE和直角△CDF中，$\left\{\begin{array}{l}{AB=CD}\\{AE=CF}\end{array}\right.$，
∴△ABE≌△CDF；
（2）∵△ABE≌△CDF，
∴BE=DF，
∴在△ADF和△CBE中，$\left\{\begin{array}{l}{AF=CE}\\{∠BEC=∠DFA}\\{BE=DF}\end{array}\right.$，
∴△ADF≌△CBE，
∴∠DAF=∠BCE，
∴AD∥BC．
点评 本题考查了全等三角新的判定与性质，证明角相等常用的方法是转化为证明三角形全等．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
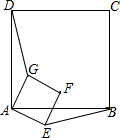如图，正方形ABCD与正方形AEFG有公共顶点A，当正方形AEFG绕着点A顺时针旋转时，在图中你能否找到一条线段与线段DG相等，并说明理由．