题目内容

6．已知a、b、c是△ABC的三边，且满足a2+c2+2b（b-a-c）=0，求△ABC各角的度数．

分析 先把原式化为（a-b）2+（b-c）2=0，再利用非负数的性质得出a=b=c，那么△ABC是等边三角形，根据等边三角形的性质即可求解．

解答 解：∵a2+c2+2b（b-a-c）=0，
∴a2+c2+2b2-2ab-2bc=0，
∴a2+b2-2ab+c2-2bc+b2=0，
即（a-b）2+（b-c）2=0，
∴a-b=0且b-c=0，即a=b且b=c，
∴a=b=c．
∴△ABC是等边三角形，
∴∠A=∠B=∠C=60°．

点评 此题考查因式分解的应用，非负数的性质，等边三角形的判定与性质，利用完全平方公式因式分解是解决问题的关键．

练习册系列答案
相关题目
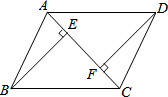16．如图，AB=CD，AF=CE，BE⊥AC于E，DF⊥AC于F．求证：
（1）△ABE≌△CDF．
（2）AD∥BC．
17．定义正整数m，n的运算：m△n=$\frac{1}{m}$+$\frac{1}{{m}^{2}}$+$\frac{1}{{m}^{3}}$+$\frac{1}{{m}^{4}}$+…+$\frac{1}{{m}^{n}}$
（1）计算3△2的值为$\frac{4}{9}$；运算“△”满足交换规律吗？回答：否（填“是”或“否”）
（2）探究：计算2△10=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{2{0}^{10}}$的值．
为解决上面的问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系的几何图形结合起来，最终解决问题．
如图所示，第一次分割，把正方形的面积二等分，其中阴影部分的面积为$\frac{1}{2}$；
第2此分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为$\frac{1}{2}$$+\frac{1}{{2}^{2}}$；
第3次分割，把上次分割图中空白部分的面积继续二等分，…；依此类推，…
第10次分割，把二次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为$\frac{1}{2}$-$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{10}}$，最后空白部分的面积是$\frac{1}{{2}^{10}}$；根据第10次分割图可以得出计算结果：$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{10}}$=1-$\frac{1}{{2}^{10}}$．
进一步分析可得出，$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$
（3）已知n是正整数，计算4△n=$\frac{1}{4}$+$\frac{1}{{4}^{2}}$+$\frac{1}{{4}^{3}}$+$\frac{1}{{4}^{4}}$+…+$\frac{1}{{4}^{n}}$的结果．
按指定方法解决问题：请仿照以上做法，只需画出第n次分割图并作标注，写出最终结果的推理步骤；或借用以上结论进行推理，写出必要的步骤．
14．羊羊运动会上，懒羊羊参加了越野比赛．选手的号码从1号开始连续编排，领号码时，懒羊羊有些迟到，工作人员警告它：“除你之外，其他选手的号码之和是180．你能推断出你的号码是多少吗？否则不让比赛！”懒羊羊的号码为（　　）
A．30B．20C．15D．10
1．如果3ab2m-1与abm+1是同类项，则m的值是2．
11．若x2+x=2，则x3+2x2-x+2015=2017．
18．先化简再求值：（$\frac{a}{{a}^{2}-{b}^{2}}$-$\frac{1}{a+b}$）÷$\frac{b}{b-a}$，其中a=sin60°，b=tan60°．
15．小强的爸爸要为公司抄写一份材料，原定每分钟抄写30个字，当抄写了材料的$\frac{2}{5}$后，决定每分钟再多抄10个字，结果提前20分钟抄完，则小强的爸爸要抄写的材料共有4000个字．
10．已知∠x等于48°12′，则∠x的余角等于41.8度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网