题目内容
8.把二次函数y=-$\frac{1}{4}$x2-x+3用配方法化成y=a(x-h)2+k的形式为y=-$\frac{1}{4}$(x+2)2+4.分析 利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑成完全平方式.
解答 解:y=-$\frac{1}{4}$x2-x+3=-$\frac{1}{4}$(x2+4x)+3=-$\frac{1}{4}$(x+2)2+4,
即y=-$\frac{1}{4}$(x+2)2+4,
∴顶点(-2,4).
故答案为:y=-$\frac{1}{4}$(x+2)2+4.
点评 此题考查了二次函数表达式的一般式与顶点式的转换,二次函数的解析式有三种形式:
(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);
(2)顶点式:y=a(x-h)2+k;
(3)交点式(与x轴):y=a(x-x1)(x-x2).

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
3. 如图,三角形ABC中,AB=AC,且AB=BD,AD=DC,则∠B的度数是( )
如图,三角形ABC中,AB=AC,且AB=BD,AD=DC,则∠B的度数是( )
 如图,三角形ABC中,AB=AC,且AB=BD,AD=DC,则∠B的度数是( )
如图,三角形ABC中,AB=AC,且AB=BD,AD=DC,则∠B的度数是( )| A. | 36° | B. | 72° | C. | 108° | D. | 144° |
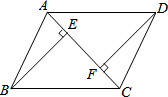 如图,AB=CD,AF=CE,BE⊥AC于E,DF⊥AC于F.求证:
如图,AB=CD,AF=CE,BE⊥AC于E,DF⊥AC于F.求证: 已知函数y=x2+2x-3的图象与x轴交于点A,B(A在B的左侧),与y轴交于点C.
已知函数y=x2+2x-3的图象与x轴交于点A,B(A在B的左侧),与y轴交于点C.