题目内容
10.下面是某同学九年级期中测验中解答的几道填空题:(1)若x2=a,则x= a ;(2)方程x(x-1)=x-1的根是 x=0 ;(3)若直角三角形的两边长为x2-3x+2=0的两个根,则该三角形的面积为 1 ;(4)若关于x的一元二次方程3x2+k=0有实数根,则 k≤0 .其中答案完全正确的个数是( )
| A. | 0个 | B. | 1个 | C. | 3个 | D. | 4个 |
分析 利用直接开平方法解方程对(1)进行判断;
根据因式分解法解方程对(2)进行判断;
根据分类讨论和勾股定理对(3)进行判断;
根据一元二次方程根的判别式对(4)进行判断.
解答 解:(1)若x2=a2,则x=±a,故错误;
(2)方程x(x-1)=x-1的根是x1=x2=1,故错误;
(3)若直角三角形的两边长为x2-3x+2=0的两个根,
∴x1=1,x2=2,则该三角形的面积为1或$\frac{\sqrt{3}}{2}$,故错误;
(4)若关于x的一元二次方程3x2+k=0有实数根,
则△=12k≥0,
∴k≥0,故错误.
故选A.
点评 本题考查了解一元二次方程-因式分解法:先把方程右边变形为0,然后把方程左边进行因式分解,这样把一元二次方程转化为两个一元一次方程,再解一次方程可得到一元二次方程的解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.要使$\sqrt{\frac{1}{x-2}}$式子有意义,字母x的取值必须满足( )
| A. | x≠0 | B. | x>2 | C. | x≠2 | D. | x≤2 |
18.下列说法中,正确的是( )
| A. | 和等于180°的两个角叫做互为余角 | |
| B. | 一个角的补角只有一个 | |
| C. | 互补的两个角一定是一个钝角和一个锐角 | |
| D. | 同角的补角相等,等角的补角也相等 |
5.在Rt△ACB中,若tanA=$\sqrt{3}$,则锐角∠A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 不能确定. |
15.一元二次方程3x2=x的解是( )
| A. | x=0 | B. | x1=0,x2=3 | C. | x1=0,x2=$\frac{1}{3}$ | D. | x=$\frac{1}{3}$ |
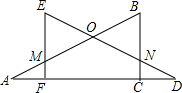 两块含30°角的全等直角三角形木板,按如图所示方式摆放,使得两条相等的直角边AC,DF在同一条直线上.此时MF与NC是否相等?请说明理由.
两块含30°角的全等直角三角形木板,按如图所示方式摆放,使得两条相等的直角边AC,DF在同一条直线上.此时MF与NC是否相等?请说明理由. 如图,AB是⊙O的弦,直线AT经过点A,且∠CAT=∠B,AT是⊙O的切线吗?为什么?
如图,AB是⊙O的弦,直线AT经过点A,且∠CAT=∠B,AT是⊙O的切线吗?为什么?