题目内容
 如图,直线y=2x-2与两坐标轴分别交于A、B两点,在x轴上取一点P,向直线
如图,直线y=2x-2与两坐标轴分别交于A、B两点,在x轴上取一点P,向直线y=2x-2作垂线,垂足为Q,使△PQA≌△BOA,求点P的坐标.
考点:全等三角形的判定,一次函数图象上点的坐标特征
专题:
分析:首先根据一次函数关系式计算出A、B两点的坐标,再根据题意画出图形,表示出AP长,根据全等三角形对应边相等可得AP=PB=1-x,然后利用勾股定理计算出P点横坐标即可.
解答: 解:如图所示:
解:如图所示:
∵直线y=2x-2与两坐标轴分别交于A、B两点,
∴A(1,0)
B(0,-2),
设P(x,0),
∴PA=1-x,
∵△PQA≌△BOA,
∴AP=PB=1-x,
∵PO2+BO2=PB2,
∴x2+22=(1-x)2,
解得:x=-
,
∴P(-
,0).
 解:如图所示:
解:如图所示:∵直线y=2x-2与两坐标轴分别交于A、B两点,
∴A(1,0)
B(0,-2),
设P(x,0),
∴PA=1-x,
∵△PQA≌△BOA,
∴AP=PB=1-x,
∵PO2+BO2=PB2,
∴x2+22=(1-x)2,
解得:x=-
| 3 |
| 2 |
∴P(-
| 3 |
| 2 |
点评:本题考查三角形全等的判定方法,以及一次函数图象上点的坐标特点,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
计算(-
)3÷(
)5的结果为( )
| 1 |
| 4 |
| 1 |
| 2 |
A、-
| ||
B、
| ||
| C、-2 | ||
| D、-1 |
 如图,太阳光线与地面成80°角,窗子AB=2米,要在窗子外面上方0.2米的点D处安装水平遮阳板DC,使光线不能直接射入室内,则遮阳板DC的长度至少是( )
如图,太阳光线与地面成80°角,窗子AB=2米,要在窗子外面上方0.2米的点D处安装水平遮阳板DC,使光线不能直接射入室内,则遮阳板DC的长度至少是( )A、
| ||
| B、2sin80°米 | ||
C、
| ||
| D、2.2cos80°米 |
 如图,AB是⊙O的弦,OC⊥OA,交AB与点P,且PC=BC,求证:BC是⊙O的切线.
如图,AB是⊙O的弦,OC⊥OA,交AB与点P,且PC=BC,求证:BC是⊙O的切线. 在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB.
在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB.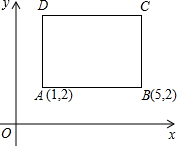 如图,四边形ABCD是一正方形,已知A(1,2),B(5,2).
如图,四边形ABCD是一正方形,已知A(1,2),B(5,2).