题目内容
若一个多边形的外角和比它的内角和少1080°,则这个多边形为 边形.
考点:多边形内角与外角
专题:
分析:根据多边形的内角和公式(n-2)•180°,外角和等于360°列出方程求解即可.
解答:解:设多边形的边数是n,
根据题意得,(n-2)•180°-360°=1080°,
解得n=10.
故答案为:十.
根据题意得,(n-2)•180°-360°=1080°,
解得n=10.
故答案为:十.
点评:本题考查了多边形的内角和公式与外角和定理,注意利用多边形的外角和与边数无关,任何多边形的外角和都是360°是解题的关键.

练习册系列答案
相关题目
|-
|=( )
| 2 |
| 11 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
下列说法正确的是( )
| A、有理数和数轴上的点一一对应 | ||||||
| B、立方根等于本身的数只有±1 | ||||||
| C、(-2)2的算术平方根是-2 | ||||||
D、-
|
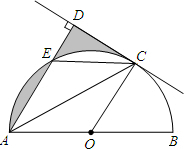 如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.
如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE. 如图,在∠1、∠2、∠3中,
如图,在∠1、∠2、∠3中, 如图,直线y=2x-2与两坐标轴分别交于A、B两点,在x轴上取一点P,向直线
如图,直线y=2x-2与两坐标轴分别交于A、B两点,在x轴上取一点P,向直线