Question

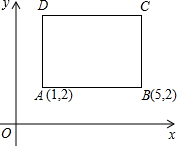如图，四边形ABCD是一正方形，已知A（1，2），B（5，2）．
（1）求点C，D的坐标；
（2）若一次函数y=kx-2（k≠0）的图象过C点，求k的值．
（3）若y=kx-2的直线与正方形ABCD有交点，求k的取值范围．

Answer 1

考点：一次函数图象上点的坐标特征,正方形的性质

专题：计算题

分析：（1）先计算出AB=4，根据正方形的性质得到AD=BC=AB=4，然后利用B点和A点坐标分别可得C点和D点坐标；
（2）把C点坐标代入y=kx-2可求出k的值；
（3）直线y=kx-2过点（0，-2），则直线y=kx-2过B点时k的值最小，过D点时对应的k的值最大．

解答：解：（1）∵A（1，2），B（5，2），
∴AB=5-1=4，AB∥x轴，
∵四边形ABCD是正方形，
∴AD=BC=AB=4，AD与BC都平行于y轴，
∴C（5，6），D（1，6）；
（2）把C（5，6）代入y=kx-2得5k-2=6，解得k=

8

5

；
（3）把D（1，6）代入y=kx-2得k-6=6，解得k=12；把B（5，2）代入y=kx-2得5k-2=2，解得k=

4

5

；
所以k的取值范围为

4

5

≤k≤12．

点评：本题考查了一次函数图象上点的坐标特征：一次函数y=kx+b，（k≠0，且k，b为常数）的图象是一条直线．它与x轴的交点坐标是（-

b

k

，0）；与y轴的交点坐标是（0，b）．直线上任意一点的坐标都满足函数关系式y=kx+b．