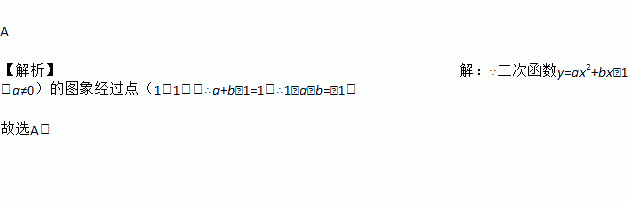题目内容
已知二次函数y=ax2+bx﹣1（a≠0）的图象经过点（1，1），则代数式1﹣a﹣b的值为（ ）
A. ﹣1 B. 2 C. ﹣3 D. 5
A
【解析】【解析】
∵二次函数y=ax2+bx﹣1（a≠0）的图象经过点（1，1），∴a+b﹣1=1，∴1﹣a﹣b=﹣1．
故选A．
如图，在△ABC中，AB=4，BC=6，DE、DF是△ABC的中位线，则四边形BEDF的周长是（ ）
A．5 B．7 C．8 D．10
D．
【解析】
试题分析：∵AB=4，BC=6，DE、DF是△ABC的中位线，∴DE=AB=2，DF=BC=3，DE∥BF，DF∥BE，∴四边形BEDF为平行四边形，∴四边形BEDF的周长为：2×2+3×2=10，故选D． 一个多边形的内角和是外角和的2倍，则这个多边形的边数为______．
6
【解析】∵多边形的外角和是360度，多边形的内角和是外角和的2倍，
则内角和是720度，
720÷180+2=6，
∴这个多边形是六边形，
故答案为：6． 某网店销售某款童装，每件售价60元，每星期可卖300件，为了促销，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件．已知该款童装每件成本价40元，设该款童装每件售价x元，每星期的销售量为y件．
（1）求y与x之间的函数关系式；
（2）当每件售价定为多少元时，每星期的销售利润最大，最大利润多少元？
（3）若该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装多少件？
（1）y=﹣30x+2100．（2）每件售价定为55元时，每星期的销售利润最大，最大利润6750元．
（3）每星期至少要销售该款童装360件．
【解析】试题分析：（1）根据售量y（件）与售价x（元/件）之间的函数关系即可得到结论．
（2））设每星期利润为W元，构建二次函数利用二次函数性质解决问题．
（3）列出不等式先求出售价的范围，再确定销售数量即可解决问题．
试题解... 如图，抛物线y=﹣x2+2x+3与y轴交于点C，点D（0，1），点P是抛物线上的动点．若△PCD是以CD为底的等腰三角形，则点P的坐标为 ．
（1+，2）或（1﹣，2）．
【解析】【解析】
∵△PCD是以CD为底的等腰三角形，∴点P在线段CD的垂直平分线上，如图，过P作PE⊥y轴于点E，则E为线段CD的中点，∵抛物线与y轴交于点C，∴C（0，3），且D（0，1），∴E点坐标为（0，2），∴P点纵坐标为2，在中，令y=2，可得，解得x=，∴P点坐标为（，2）或（，2），故答案为：（，2）或（，2）． 在下列y关于x的函数中，一定是二次函数的是（ ）
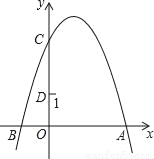
A. y=2x2 B. y=2x﹣2 C. y=ax2 D.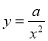 
A
【解析】解：A．是二次函数，故A符合题意；
B．是一次函数，故B错误；
C．a=0时，不是二次函数，故C错误；
D．a≠0时是分式方程，故D错误；
故选A． 如图，有一座抛物线形拱桥，在正常水位时水面AB的宽为20m，如果水位上升3m时，水面CD的宽是10m，建立如图所示的直角坐标系，则此抛物线的解析式为___________．
y＝－x2
【解析】【解析】
设抛物线解析式为y=ax2，因为抛物线关于y轴对称，AB=20，所以点B的横坐标为10．设点B（10，n），点D（5，n+3），由题意得： ，解得： ，∴．
故答案为： ． 袋中有5个红球，6个白球，12个黑球，每个球除颜色外都相同，事先选定一种颜色，若摸到的球的颜色与事先选定的一样，则获胜，否则就失败，为了尽可能获胜，你事先应选择的颜色是__．
黑色
【解析】先分别求出摸到红球，白球，黑球的概率，再比较它们的大小，概率最大的即为所求．
【解析】
∵袋中有5个红球，6个白球，12个黑球，
∴袋中一共有球：5+6+12=23（个），
∴摸到红球的概率为： ，
摸到白球的概率为： ，
摸到黑球的概率为： ，
又∵＜＜，
∴摸到黑球的概率最大，会尽可能获胜．
故答案为黑球． 在平面直角坐标系中，线段OP的两个端点坐标分别为O（0，0），P（4， 3），将线段OP绕点O逆时针旋转90°到OP′位置，则点P′的坐标是（ ）
A．（3，4） B．（－4，3） C．（－3，4） D．（4，－3）
C．
【解析】
试题分析：如图，OA=3，PA=4，
把线段OP绕点O逆时针旋转90°到OP′位置可得OA旋转到x轴负半轴OA′的位置，OB旋转到y轴正半轴OB′的位置,所以P′A′=PA=4，P′B′=PB=3,即可得P′点的坐标为（﹣3，4）．故答案选C．