题目内容
19.为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对全市5万名学生参加户外活动的时间进行抽样调查,并将调查结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题: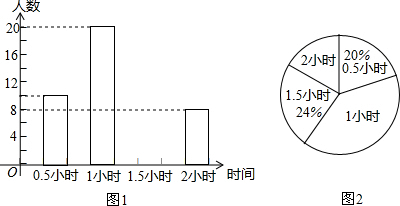
(1)在这次调查中共调查了多少名学生?
(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;
(3)求表示户外活动时间2小时的扇形圆心角的度数;
(4)本次调查中学生参加户外活动的平均时间是否符合要求?估计全市有多少学生参加户外活动的时间符合要求.
分析 (1)根据统计图找出活动时间为0.5小时的人数和百分比,计算得到答案;
(2)求出户外活动时间为1.5小时的人数,补充频数分布直方图;
(3)根据在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比解答即可;
(4)求出参加户外活动的平均时间比较即可得到答案.
解答 解:(1)由直方图可知,活动时间为0.5小时的人数是10人,由扇形图可知活动时间为0.5小时的人数占20%,
则调查人数为:10÷20%=50(人);
(2)户外活动时间为1.5小时的人数:50×24%=12(人);
频数分布直方图如图: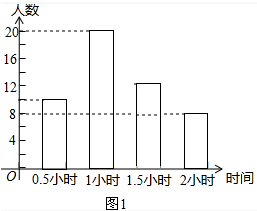
(3)表示户外活动时间2小时的扇形圆心角的度数=$\frac{8}{50}$×360°=57.6°,
(4)户外活动的平均时间=$\frac{10×0.5+20×1+12×1.5+8×2}{50}=1.18$(小时).
∵1.18>1,∴平均活动时间符合上级要求;
全市参加户外活动时间符合要求的学生为:$\frac{20+12+8}{50}×50000=40000$(人).
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.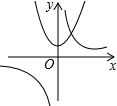 如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}-{x}^{2}$-1>0的解集是( )
如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}-{x}^{2}$-1>0的解集是( )
 如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}-{x}^{2}$-1>0的解集是( )
如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}-{x}^{2}$-1>0的解集是( )| A. | x>1 | B. | x<-1 | C. | 0<x<1 | D. | -1<x<0 |