题目内容
13. 如图,在△ABC中,AB=AC=2,点P在BC上.若点P为BC的中点,则m=AP2+BP•PC的值为4;若BC边上有100个不同的点P1,P2,…,P100,且mi=APi2+BPi•PiC(i=1,2,…,100),则m=m1+m2+…+m100 的值为400.
如图,在△ABC中,AB=AC=2,点P在BC上.若点P为BC的中点,则m=AP2+BP•PC的值为4;若BC边上有100个不同的点P1,P2,…,P100,且mi=APi2+BPi•PiC(i=1,2,…,100),则m=m1+m2+…+m100 的值为400.
分析 第一个空,由等腰三角形的三线合一性质和勾股定理得出AP2+BP•PC=AB2即可;
第二个空,作AD⊥BC于D.根据勾股定理,得APi2=AD2+DPi2=AD2+(BD-BPi)2=AD2+BD2-2BD•BPi+BPi2,PiB•PiC=PiB•(BC-PiB)=2BD•BPi-BPi2,从而求得mi=AD2+BD2,即可求解.
解答 解:若点P为BC的中点,如图1所示:
AB=AC=2,
∴AP⊥BC,BP=CP,
∴∠APB=90°,
∴AP2+BP•PC=AP2+BP2=AB2=4.
若BC边上有100个不同的点P1,P2,…,P100,
作AD⊥BC于D,则BC=2BD=2CD,如图2所示.
根据勾股定理,得
APi2=AD2+DPi2=AD2+(BD-BPi)2=AD2+BD2-2BD•BPi+BPi2,
又∵PiB•PiC=PiB•(BC-PiB)=2BD•BPi-BPi2,
∴m1=AD2+BD2=AB2=4,
∴m1+m2+…+m100=4×100=400.
故答案为:4,400.
点评 此题主要运用了勾股定理和等腰三角形三线合一的性质;作辅助线构造直角三角形是解本题的突破点,另外代入进行整理后代换出PC也是同学们不容易考虑到的.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
3.一元二次方程x(x-3)=0根是( )
| A. | x1=3,x2=0 | B. | x=-3 | C. | x1=-3,x2=0 | D. | x=3 |
 如图,已知有理数a,b对应数轴上两点A,B.为让算式-12-|a□b|计算出来的值最大,算式中的□所在位置应选择的运算符号是( )
如图,已知有理数a,b对应数轴上两点A,B.为让算式-12-|a□b|计算出来的值最大,算式中的□所在位置应选择的运算符号是( )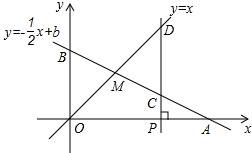 如图所示,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C,D.
如图所示,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C,D.  如图,D、E、F和A、B、C分别在同一直线上,若∠1=∠2,∠C=∠D,求证:∠A=∠F.
如图,D、E、F和A、B、C分别在同一直线上,若∠1=∠2,∠C=∠D,求证:∠A=∠F.