题目内容
先请阅读下列题目和解答过程:
“已知a,b,c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
解:因为a2c2-b2c2=a4-b4①,
所以c2(a2-b2)=(a2+b2)(a2-b2)②,
所以c 2=a2+b2③,
2=a2+b2③,
所以△ABC是直角三角形④.”
请解答下 列问题:
列问题:
( 1)上列解答过程,从第几步到第几步出现错误?
1)上列解答过程,从第几步到第几步出现错误?
(2)简要分析出现错误的原因.
(3)写出正确的解答过程.
【解析】(1)从第②步到第③步出错.
(2)等号两边不能同除以a2-b2,因为它有可能为零.
(3)因为a2c2-b2c2=a4-b4,
所以c2(a2-b2)=(a2+b2)(a2-b2),
移项得:c2(a2-b2)-(a2+b2)(a2-b2)=0,
得(a2-b2)(c2-a2-b2)=0,
所以a2=b2或c2=a2+b2,
所以△ABC是直角三角形或等腰三角形或等腰直角三角形.

练习册系列答案
相关题目
八年级一、二班的同学在一次数学测验中的成绩统计情况如下表:
| 班级 | 参加人数 | 中位数 | 平均数 | 方差 |
| 一 | 50 | 84 | 80 | 186 |
| 二 | 50 | 85 | 80 | 161 |
某同学分析后得到如下结论:①一、二班学生的平均成绩相同;②二班优生人数多于一班(优生线85分);③一班学生的成绩相对稳定.其中正确的是( )
A.①② B.①③ C.①②③ D.②③
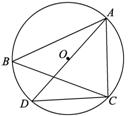
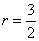 ,AC=2,则cosB的值是( )
,AC=2,则cosB的值是( )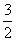
 B.
B.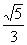 C.
C.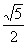 D.
D.

 C.C点 D.D点
C.C点 D.D点 0°,∠2=50°,则∠ABC= 度.
0°,∠2=50°,则∠ABC= 度.

